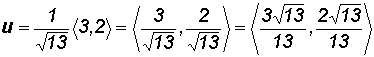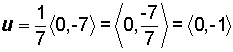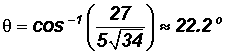Examples

INTRODUCTION TO VECTORS - PART 2

Example 1:

Let v = < 2, 5 > and w = < 3, 4 >, find the dot product v w.

v w = 2(3) + 5(4)

= 6 + 20

= 14 which is a scalar!

Example 2:

Find a unit vector u in the direction of v = < 3, 2 >.

Given the formula we need to find the magnitude of vector v.

Given ||v|| = , we find ||v|| =

It follows that

Note: We just found a unit vector for the vector v drawn in Example 1. It lies on top of vector v and has a "length" of 1. Incidentally, we found the magnitude of vector v already in Example 3.

Example 3:

Find a unit vector in the direction of v = < 0, 7 >.

Given the formula we need to find the magnitude of vector v.

Given ||v|| = , we find ||v|| =

It follows that

Example 4:

Write the following vectors in terms of the standard unit vectors i and j:

(a) v = < 2, 5 >

Please note that a vector written in component form does not include the i and j unit vector and the horizontal and vertical components are separated by commas.

v = 2i + 5j

Please note that a vector written in terms of the i and j unit vector is neither in angle brackets nor are the horizontal and vertical components separated by commas.

(b) w = < 5, 1 >

w = 5i j

(c)   a = < 7, 0 >

    a = 7i

(d) b = < 0, 10 >

      b = 10j

(e) u = < 6, 2 >

u = 6i 2j

(f) n = < 6, 2 >

n = 6i + 2j

Example 5:

Find the angle between z = < 4, 3 > and w= < 3, 5 > and round to 1 decimal place.

Using the formula , lets find

||z|| =

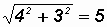
||w|| =

and then the dot product

zw = 4(3) + 3(5) = 27

Then

and

NOTE: During the process of solving for the angle always try to use given values without rounding first.

Example 6:

Given the following vectors, determine whether they are parallel, orthogonal or neither.

(a)   u = < 6, 4 > and v = < 2, 3 >

Parallel:

Two nonzero vectors u and v are parallel if there is some scalar c such that u = cv. Therefore, can we factor a scalar out of vector u so that the remaining vector is equal to vector v?

That is, < 6, 4 > = 2 < 3, 2 >. Since < 3, 2 > is not equal to < 2, 3 >, we can state that vectors u and v are NOT parallel.

Orthogonal:

Remember that two vectors u and v are orthogonal if the dot product equals 0.

Since u v = 6(2) + 4(3) = 0, we can state that vectors u and v are orthogonal.

(b)   u = < 9, 15 > and v = < 3, 5 >

Parallel:

Since < 9, 15 > = 3 < 3, 5 >, we can see that vector u is a multiple of vector v. This means that the vectors are parallel.

(c)   u = < 1, 3 > and v = < 0, 5 >

Parallel:

It should be obvious that there is no scalar that allows us to state that u = cv. We can say with confidence that vectors u and v are NOT parallel.

Orthogonal:

Since u v = 1(0) + 3(5) = 15, we can state that vectors u and v are NOT orthogonal because the dot product does NOT equal 0.