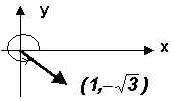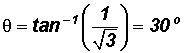INTRODUCTION TO VECTORS - PART 1

Example 1:

Let w be a vector in a rectangular coordinate system with initial point P at (1, – 3) and terminal point Q at (– 5, 3).  Write the vector v in component form.

Basically, we are asked to place the vector into standard position.  We will use the formula < x₂ – x₁ , y₂ – y₁ > ("terminal minus initial") which is the component form of a vector that has been moved from somewhere in the coordinate system to standard position.  While developing the formula, we assigned the coordinates (x₁, y₁) to the initial point P and (x₂, y₂) to the terminal point Q.

Therefore, the component form of vector w must be < – 5 – 1, 3 – (– 3) >.  Simplifying, we find the component form of vector w to be < – 6, 6 >.

Example 2:

Calculate the EXACT magnitude of v = < 3, 2 >.

Given ||v|| = , we find ||v|| =

Example 3:

Calculate the EXACT magnitude of v = < 0, 7 >.

Given ||v|| = , we find ||v|| =

Example 4:

Calculate the EXACT magnitude of v = < 4, 3 >.

Given ||v|| = , we find ||v|| =

Example 5:

Calculate the EXACT magnitude of v = < 8, 0 >.

Given ||v|| = , we find ||v|| =

Example 6:

Find the direction angle of vector .

Let's look at a picture of the vector and its direction angle. Remember that a direction angle is positive and measured from the positive x-axis to the vector in standard position as shown below!

From earlier work we know that , therefore, we find

and

Looking at the graph of the vector, we know that we are required to find a positive angle whose terminal side is in Quadrant IV.

We will use the Reference Angle of 60^o which is 60^o to find that the direction angle must equal 300^o.

Example 7:

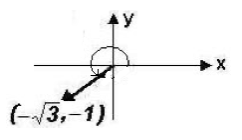
Find the direction angle of vector .

Let's look at a picture of the vector and its direction angle.Remember that a direction angle is positive and measured from the positive x-axis to the vector in standard position as shown below!

Knowing that , we can find

and

Looking at the graph of the vector, we know that we are required to find a positive angle whose terminal side is in Quadrant IV. We will use the Reference Angle of 30^o which is 30^o to find that the direction angle must equal 210^o.

Example 8:

Let v = < 2, 5 > and w = < 3, 4 >.  Find the following:

(a)  v + w = < 2, 5 > + < 3, 4 >

                  = < 2 + 3, 5 + 4>

                  = < 1, 9>

(b)  2v

      2v = 2< 2, 5 >

           = < 4, 10 >

(c)  w v

      w v = < 3, 4 > < 2, 5 >

                = < 3 (2), 4 5 >

                = < 5, 1 >

(d)  v + 2w

      v + 2w = < 2, 5 > + 2< 3, 4 >

                  = < 4, 13 >