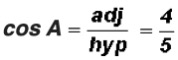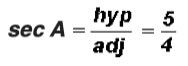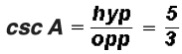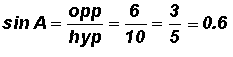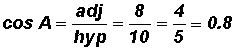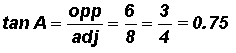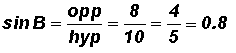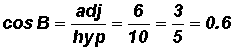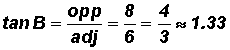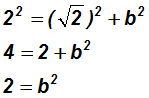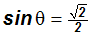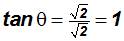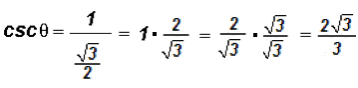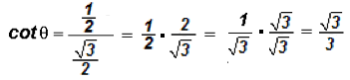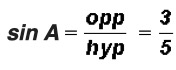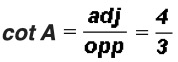THE SIX TRIGONOMETRIC RATIOS

Example 1:

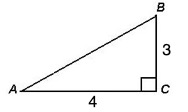
Given the following triangle, find the numeric values of the sine, cosine, and tangent ratios of angles A and B.  Express your answers both as a fraction and a decimal.

Ratios for Angle A:

Ratios for Angle B:

Please note that the location of the "side opposite" and the" side adjacent" changes with the location of the angle in the triangle.  The numeric values for the trigonometric ratios of angle A are different from the numeric values of the trigonometric ratios of angle B. 

Example 2:

Given , use appropriate trigometric ratios to find the exact value of the sine and tangent ratios of angle.

Knowing that , we also know the following:

adj (side adjacent to the angle ) is units in length

hyp (hypotenuse) is 2 units in length

We can now find opp (side opposite the angle ) by using the Pythagorean Theorem NOTE: Unless you are told otherwise, c is always the hypotenuse of a right triangle and a and b are the legs.

Let's find opp (side opposite the angle).  Let's assume that it is b in the Pythagorean Theorem! 

Now we'll use the Square Root Property to find the length of b = opp:

 

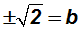
Since we are working with a right triangle whose sides are never negative, we find

b = opp =

Now we are ready to find the sine and cosine ratios given opp = , adj = , and hyp = 2.

Reminder:                              

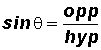
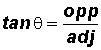
Example 3:

Given a right triangle for which and , use the Reciprocal and Quotient Identities to find the remaining four trigonometric ratios.

Let's use the Reciprocal Identities and to find the ratios for cosecant and secant.

Then and .

Please note that there is a radical in the denominator of the cosecant. While this is usually a "no-no" in algebra, in trigonometry it is okay to leave the radical in the denominator.

If you do want to rationalize the denominator, you must multiply the numerator and denominator by as follows:

Let's use the Quotient Identities and to find the ratios for tangent and cosecant.

Then and .

Please note that there is a radical in the denominator of the cotangent. If you do want to rationalize the denominator, you must multiply the numerator and denominator by as follows:

Example 4:

Given a right triangle for which , find the ratios of the other five trigonometric ratios.

Knowing that , we can make the following picture:

We can find the length of the hypotenuse c by using the Pythagorean Theorem.

Using the Square Root Property, we can solve for c as follows:

Since we are working with a right triangle whose sides are never negative, we can state that c = 5.

Now we can find the other trigonometric ratios.