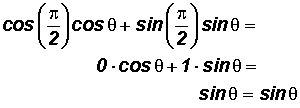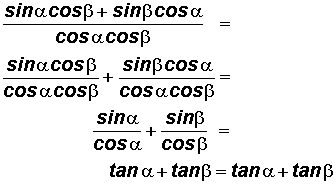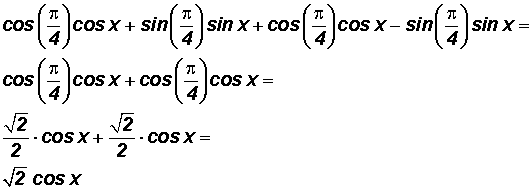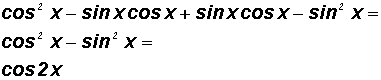SUM AND DIFFERENCE IDENTITIES
DOUBLE ANGLE AND HALF ANGLE IDENTITIES

Example 1:

Show that can be changed to sin.

Let's use the Difference Identity for Cosine .

Here, u and v .

Your calculator must be in radian mode!

We showed that equals sin.

Example 2:

Show that can be changed to .

Let's use the Sum Identity for Sine .

Here, u and v .

We showed that equals.

Example 3:

Simplify .

Let's use the Sum and Difference Identities of Cosine

and .

Here, u and v x.

 

We showed that can be simplified to .

Example 4:

Simplify using the Double Angle Identity .

Let's factor out a 3 to get .

We showed that can be written as 3 sin2x.

Example 5:

Simplify using the Double Angle Identity .

Let's factor out a 4 to get

We showed that can be written as 4 cos2x.

Example 6:

Simplify using the Double Angle Identity .

Here, u x.

Let's multiply the parentheses using FOIL to get

We showed that can be written as cos 2x.

Example 7:

Simplify using the Half Angle Identity .

We can see that u 6x, therefore 3x.

Using the pattern of the Half Angle Identity, we can write as sin 3x.

Example 8:

Simplify using the Half Angle Identity.

We can see that u 4x, therefore 2x .

Using the pattern of the Half Angle Identity, we can write as cos 2x.

Example 9:

Rewrite in terms of a Double Angle Identity and a Half Angle Identity:

Using :

We can see that 2u 6x, therefore u 3x.

Using the pattern of the Double Angle Identity, we can write as 2 sin 3x cos 3x.

Using :

We can see that 6x, therefore u 12x.

Using the pattern of the Half Angle Identity, we can write as .