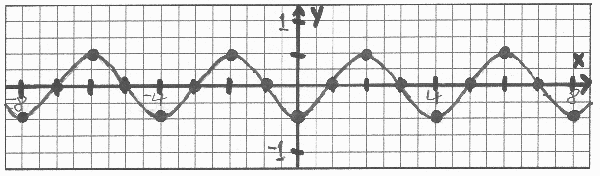
SINE AND COSINE FUNCTIONS

Example 1:    

Given g(x) = 2 sin(2x), do the following:

a.   State the amplitude,

The amplitude is |2| = 2. This means that the y-values of the peaks are 2 and the y-values of the valleys are 2. No larger and smaller y-values exist.

b.   State the EXACT period.

Since b = 2, the period is .  This means the representative picture is units in length.

c.   Sketch the function on the interval by hand.

(1) Keep in mind the graph and characteristics of the basic sine function!

(2) Mark off a distance along the x-axis starting at the origin to represent the period .

(3) Divide this period into four equal intervals. Each will be of length /4. 

(4) Create the representative picture by using the beginning and ending point of each interval.

Note that the x-values are integer multiples of /4 and the y-values must be calculated using the x-values. Use a calculator!

Specifically, the points will be (0, 0), (/4, 2), (2/4 = /2, 0), (3/4, 2), and (, 0).

(5) Connect the points to form the representative picture of the sine function. 

(6) Copy several more cycles in the same manner to the right and left of the representative pictureon the interval . 

Please note that the peaks and valleys in the graphs of the sine functions are U-shaped!

Note that the units along the x-axis are DIFFERENT from the units along the y-axis!  As long as you place numbers along your axes it does not matter "how long" your units are!

Example 2:    

Given , do the following:

a.   State the amplitude.

The amplitude is . This means that the y-values of the peaks are and the y-values of the valleys are . No larger and smaller y-values exist.

Please note that a is negative! This means that the representative picture is reflected in the x-axis. Instead of drawing a peak first, we will draw a valley instead!

b.   State the EXACT period.

Since b = , the period is .  This means the representative picture is 2 units in length.

c.   Sketch the function on the interval by hand.

(1) Keep in mind the graph and characteristics of the basic sine function!

(2) Mark off a distance along the x-axis starting at the origin to represent the period 2.

(3) Divide this period into four equal intervals. Each will be of length 2/4 = 1/2. 

(4) Create the representative picture by using the beginning and ending point of each interval.

Note that the x-values are integer multiples of 1/2 and the y-values must be calculated using the x-values. Use a calculator!

Specifically, the points will be (0, 0), (1/2, 1/2), (2/2 = 1, 0), (3/2, 1/2), and (2, 0).

Please note that "a" is negative! This means that the representative picture is reflected in the x-axis. Instead of drawing a peak first, we will draw a valley instead!

(5) Connect the points to form the representative picture of the sine function. 

(6) Copy several more cycles in the same manner to the right and left of the representative picture on the interval .  

Please note that the peaks and valleys in the graphs of the sine functions are U-shaped!

Note that the units along the x-axis are DIFFERENT from the units along the y-axis!  As long as you place numbers along your axes it does not matter "how long" your units are!

Example 3:    

Given , do the following:

a.   State the amplitude.

The amplitude is |2| = 2. This means that the y-values of the peaks are 2 and the y-values of the valleys are 2. No larger and smaller y-values exist.

b.   State the EXACT period.

Since b = , the period is .  This means the representative picture is 4units in length.

c.   Sketch the function on the interval by hand.

(1) Keep in mind the graph and characteristics of the basic cosine function!

(2) Mark off a distance along the x-axis starting at the origin to represent the period 4.

(3) Divide this period into four equal intervals. Each will be of length 4/4 = . 

(4) Create the representative picture by using the beginning and ending point of each interval.

Note that the x-values are integer multiples of and the y-values must be calculated using the x-values. Use a calculator!

Specifically, the points will be (0, 2), (, 0), (2, 2), (3, 0), and (4, 2).

(5) Connect the points to form the representative picture of the cosine function. 

(6) Copy several more cycles in the same manner to the right and left of the representative picture on the interval . 

Please note that the peaks and valleys in the graphs of the cosine functions are U-shaped!

Note that the units along the x-axis are DIFFERENT from the units along the y-axis!  As long as you place numbers along your axes it does not matter "how long" your units are!

Example 4:    

Given , do the following:

a.   State the amplitude.

The amplitude is . This means that the y-values of the peaks are and the y-values of the valleys are . No larger and smaller y-values exist.

Please note that a is negative! This means that the representative wave is reflected in the x-axis. Instead of drawing a peak first, we will draw a valley instead!

b.   State the EXACT period.

Since b = /2, the period is .  This means the representative picture is 4 units in length.

c.   Sketch the function on the interval by hand.

(1) Keep in mind the graph and characteristics of the basic cosine function!

(2) Mark off a distance along the x-axis starting at the origin to represent the period 4 .

(3) Divide this period into four equal intervals. Each will be of length 4/4 = 1. 

(4) Create the representative picture by using the beginning and ending point of each interval.

Note that the x-values are integer multiples of 1 and the y-values must be calculated using the x-values. Use a calculator!

Specifically, the points will be (0, 1/2), (1, 0), (2, 1/2), (3, 0), and (4, 1/2).

Please note that "a" is negative! This means that the representative picture is reflected in the x-axis. Instead of drawing a peak first, we will draw a valley instead!

(5) Connect the points to form the representative picture of the cosine function. 

(6) Copy several more cycles in the same manner to the right and left of the representative picture on the interval . 

Please note that the peaks and valleys in the graphs of the cosine functions are U-shaped!

Note that the units along the x-axis are DIFFERENT from the units along the y-axis!  As long as you place numbers along your axes it does not matter "how long" your units are!

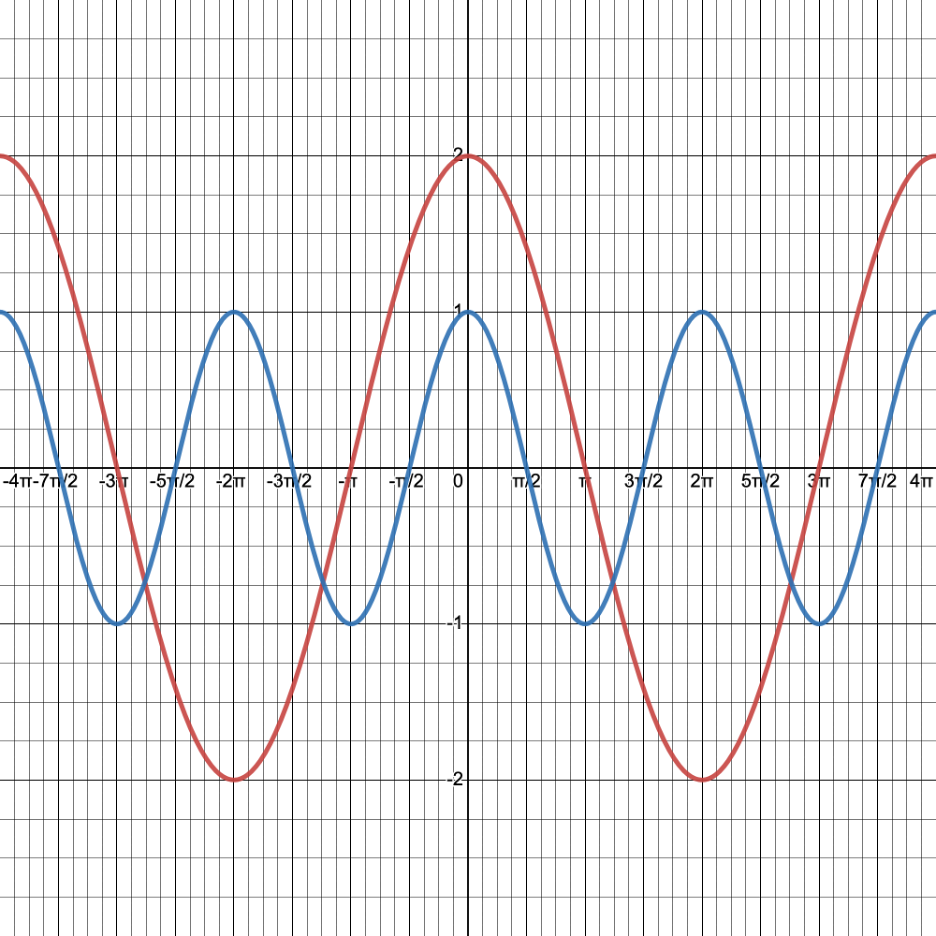
Example 5:

Use Desmos at https://www.desmos.com/calculator to draw the graph of y = cos(x) and that of its transformation into the same coordinate system.

Required Graph Characteristics:

1. Show the representative picture and a copy of one to the right of it.
2. Place numbers on both axes.
3. The x-axis numbers must contain . The beginning/ending point of each interval in each copy of the representative picture must show numbers.
4. The y-axis numbers must show the appropriate values for the x-axis numbers used in (3).
5. Do not make the y-axis too large. We need to see the peaks and valleys clearly!

You can find instructions for Desmos at http://profstewartmath.com/Math127/A_CONTENTS/desmos.htm

Since b = , the period is .  This means the representative picture is 4units in length. This knowledge will allow us to find the required x-values.

Since the amplitude is |2| = 2, let's restrict the y-axis to between 3 and 3 in the Desmos "Graph Settings". One integer more than the amplitude is enough!

NOTE:

Sometimes, we have to try different settings in the Desmos "Graph Settings" window before the required x-axis numbers show up. Additionally, when we export the image, we need to determine which size best shows all required characteristics.

In the graph above, the Desmos "Graph Settings" for the x-axis are between 4 and 4 and the Step is /2.

The "Large Square" size was used for Desmos image export. Incidentally, the other settings refused to show all of the x-axis numbers.