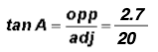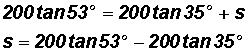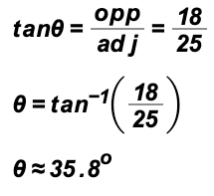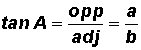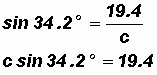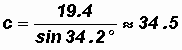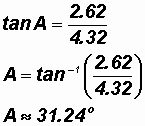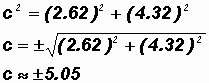RIGHT TRIANGLE TRIGONOMETRY

Example 1:

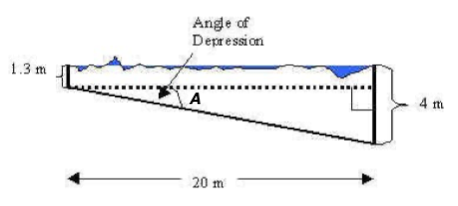
A swimming pool is 20 meters long. The bottom of the pool has a constant slant so that the water depth is 1.3 meters at the shallow end and 4 meters at the deep end. Find the angle of depression of the bottom of the pool rounded to two decimal places.

For our calculations we are going to use the right triangle shown in the picture. The side opposite the angle A is 4 1.3 = 2.7 m and the side adjacent to the angle A is 20 m.

Using the tangent function, we find that

and then

The angle of depression is approximately 7.69^o.

NOTE: In mathematics, we usually try to work with exact numbers as long as possible. In this problem, the fraction is considered to be more exact than its decimal equivalent because it may end up being a rounded value.

Example 2:

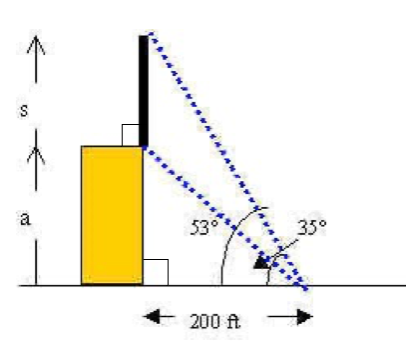
A building of height a has an antenna attached to its flat roof at a right angle. It is considered an extension of the side of the building! At a point 200 feet from the base of the building, the angle of elevation to the bottom of the antenna is 35^o, and the angle of elevation to the top of the antenna is 53^o. Find the height s of the antenna rounded to one decimal place.

Note from the picture that this problem involves two right triangles. Incidentally, we are assuming the building makes a right angle with the ground!

We are going to use to find the height s of the antenna.

However, we need to find the height a of the building first. For this, we will use .

We conclude that the height of the building is a = 200 tan 35^o.

At this point, we will not show the decimal approximation for the height of the building. In mathematics, we usually try to work with exact numbers as long as possible. Therefore, we try not to round until the final calculation.

Now, given , we will use to conclude that the height s of the antenna is as follows:

 

We will input the above calculation into a calculator in its entired to find that s 125.4 (here we can finally round!).

Thus, the height of the antenna is approximately 125.4 feet.

Example 3:

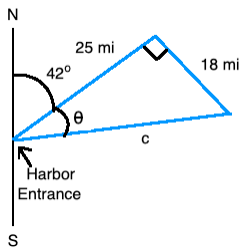
A boat leaves the entrance to a harbor and travels 25 miles on a bearing of N 42^o E. The boat captain then turns the boat 90^o clockwise and travels another 18 miles.

a. After these maneuvers, how far is the boat from the harbor entrance? Round to the nearest tenth of a mile.

We must find distance c in the picture. We can use the Pythagorean Theorem.

Now using the Square Root Property, we get

Since the side of a triangle is never negative, the length of side c is strictly about 30.8 miles, which is the distance of the boat to the entrance of the harbor

b. What is the bearing of the boat from the harbor entrance? Round to the nearest tenth of a degree.

See picture above. The angle in the bearing we are asked to find is 42^o + .

Because we are measuring this angle from the north side of the north-south line (positive y-axis) and the boat is east of the harbor, its bearing from the harbor entrance is N (42^o + ) E.

We need to find . We will use the tangent ratio since we are working with a right triangle.

Note, we did not use the cosine or sine ratio because then we would have had to work with c (hypotenuse), which is a rounded value.

We find 42^o + 42^o + 35.8^o = 77.8^o. Therefore, the bearing of the boat from the harbor entrance is approximately N 77.8^o E.

Example 4:

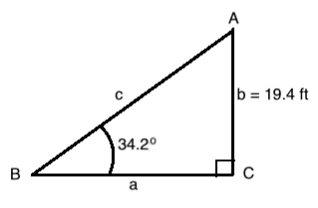
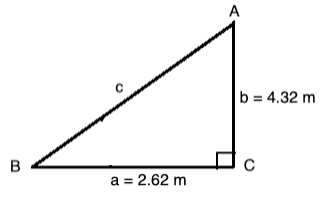
Solve the right triangle pictured below. That is, find all unknown sides and angles. Round the final solutions to one decimal place!

Solve for Angle A:

Since the sum of the interior angles of a triangle always equals 180^o we find that

A = 180^o90^o 34.2^o = 55.8^o

Solve for Side a:

Let's use the fact that

In our case,

and

Solve for Side c:

Let's use the fact that because then we do not have to use a previously rounded value (side a), something we should avoid if at all possible.

In our case,

and

We find that A = 55.8^o, a 28.5 ft, and c 34.5 ft