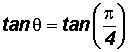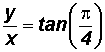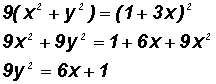Examples

POLAR EQUATIONS

Example 1:

Change the rectangular equation to polar form. Write the polar equation as r in terms of .

Knowing that and , we can convert as follows:

Now, we must write r in terms of .

In this case, this is done by factoring. We will factor r out of both expressions to get

Using the Zero Product Principle we get

or .

The graph of is the pole.

Since the pole is already included in (Hint: Let = 0), we don't need .

Therefore, all we need to do is write in terms of .

That is, .

Thus, the polar form of is .

WARNING:

It is incorrect to divide both sides of the equation by r to arrive at the solution !!! From algebra you should remember that we cannot divide by a variable UNLESS we are certain that this variable will NEVER take on the value of 0. In our case, we find thatr actually can take on this value!

Example 2:

Change the rectangular equation to polar form. Write the polar equation as r in terms of .

Knowing that and , we can convert as follows:

Now, we must write r in terms of . In this case, this is done by factoring. We will factor r out of both expressions to get

Next, we will factor r out of both expressions as follows:

Using the Zero Product Principle we get

or

The graph of is the pole. Since the pole is already included in the graph of (Hint: Let = 0), we don't need .

Therefore, all we need to do is write in terms of .

That is, .

Thus, the polar form of is .

Example 3:

Change the rectangular equation to polar form. Write the polar equation as r in terms of .

Knowing that , we can convert as follows:

It may seem to you that we have accomplished our goal, that is, we converted the rectangular equation to polar form. However, it is standard procedure to write r in terms of .

Now, we must write r in terms of . In this case, this is done by factoring as follows:

and (Notice that we are dealing with a Difference of Squares).

Using the Zero Product Principle we get

or

Next, we will rewrite the polar equation as r in terms of .

That is, or

Either of the two equations is correct. However, it is accepted mathematical practice to let the positive value,, represent in polar form.

Remember that the variables in a polar equation are r and ! Only having an r-value means that it is held constant while the angle can take on any value.

Example 4:

Change the rectangular equation to polar form. Write the polar equation as r in terms of .

Knowing that , we can convert as follows:

Now, we must write the polar equation as r in terms of . All we have to do is divide both sides of the equation by sin.

or (Both solutions are acceptable!)

Thus, the polar form of is either or .

Example 5:

Change the polar equation to rectangular form.

In this case, we will multiply both sides of the equation by r to get

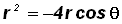
Knowing that and , we can convert as follows:

Thus, the rectangular form of is .

Example 6:

Change the polar equation to rectangular form.

Since we do not have a formula that converts r to rectangular form, we will raise both sides to the second power to get

Now we can use the formula to get .

Thus, the rectangular form of is .

Example 7:

Change the polar equation to rectangular form.

Since we do not have a formula that converts to rectangular form, we will place the "tan" in front of both sides of the equation as follows:

We can use the formula to get

and or (Both solutions are acceptable!)

Thus, the rectangular form of is or .

Example 8:

Change the polar equation to rectangular form.

Since we do not have a formula that converts secant to to rectangular form, we will use a Reciprocal Identity as follows:

Next, let's multiply both sides by , so that we get

Knowing that , we can convert as follows:

Thus, the rectangular form of is .

Example 9:

Convert the polar equation to a rectangular equation.

Since we do not have a formula that converts r to rectangular form, we'll multiply both sides of the equation by the denominator of the term on the right of the equal sign to get

r(3 3cos) = 1

then 3r 3rcos = 1

and 3r = 1 + 3cos

Next, we'll square both sides to get

and given that and , we can now write

Thus, the rectangular form of is 9y² = 6x + 1.