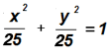INTRODUCTION TO PARAMETRIC EQUATIONS

Example 1:

Find a set of parametric equations for the function y = 1 x² use the parameter t.

This is a quadratic function and its graph is a parabola.

Step 1:

Use the parameter t

Step 2:

Let x = t

Step 3: Express y in terms of the parameter

y = 1 (t²) = 1t²

In conclusion, the set of parametric equations consists of x = t and y = 1t².

This can also be expressed as an ordered pair as ( t, 1t²) where the first expression indicates the x-coordinates of all points on the graph of the function y = 1 x² and the second expression indicates the y-coordinates.

Investigate the direction of movement by graphing the set of parametric equations in desmos.com! For example, you would input ( t, 1t²). Then replace t on the left with 10 and on the right with increasingly larger numbers starting at, say, at 1.

Watch the curve develop from right to left.

Example 2:

Let's use the function y = 1 x² again, but this time we will use the parameter t.

Step 1:

Use the parameter t

Step 2:

Let x = t

Step 3: Express y in terms of the parameter

y = 1t²

In conclusion, the set of parametric equations consists of x = t and y = 1t².

This can also be expressed as an ordered pair as (t, 1t²) where the first expression indicates the x-coordinates of all points on the graph of the function y = 1 x² and the second expression indicates the y-coordinates.

Investigate the direction of movement by graphing the set of parametric equations in desmos.com! For example, you would input (t, 1t²). Then replace t on the left with 10 and on the right with increasingly larger numbers starting at, say, at 1.

Watch the curve develop from left to righ.

Example 3:

Find a set of parametric equations for the ellipse 4x² + 9y² = 36 where .

This ellipse has its center at the origin.

Step 1:

Change the equation to standard form. Let's first divide both sides by 36 and reduce to get

This can be written as .

Step 2:

We will now use the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1.

We are given . But we can also see this by relating the Pythagorean Identity to the standard form in Step 1.

Expressed in terms of x, this is x = 3sin(t). This is our first parametric equation.

It follows that .

Expressed in terms of y, this is y = 2cos(t). This is our second parametric equation.

In conclusion, she set of parametric equations consists of x = 3sin(t) and y = 2cos(t).

NOTE: The direction of movement along the curve is clockwise. Convince yourself of this by graphing the set of parametric equations in desmos.com! For example, you would input (3 sin(t), 2 cos(t) ). Then replace t with increasingly larger positive numbers and watch the curve develop in clockwise direction.

Example 4:

Find a set of parametric equations for the ellipse 4x² + 9y² = 36 again, but this time let .

Step 1:

Change the equation to standard form. Let's first divide both sides by 36 and reduce to get

This can be written as .

Step 2:

We will now use the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1.

We are given . But we can also see this by relating the Pythagorean Identity to the standard form in Step 1.

Expressed in terms of y, this is y = 2sin(t). This is our first parametric equation.

It follows that .

Expressed in terms of x, this is x = 3cos(t). This is our second parametric equation.

In conclusion, she set of parametric equations consists of x = 3cos(t) and y = 2sin(t).

NOTE: The direction of movement along the curve is counter-clockwise. Convince yourself of this by graphing the set of parametric equations in desmos.com! For example, you would input (3 cos(t), 2 sin(t) ). Then replace t with increasingly larger positive numbers and watch the curve develop in counter-clockwise direction.

Example 5:

Find a set of parametric equations for the circle x² + y² = 25 where .

This circle has its center at the origin.

Step 1:

Change the equation to standard form. Let's first divide both sides by 25 and reduce to get

This can be written as.

Step 2:

We will now use the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1.

We are given . But we can also see this by relating the Pythagorean Identity to the standard form in Step 1.

Expressed in terms of x, this is x = 5sin(t). This is our first parametric equation.

It follows that .

Expressed in terms of y, this is y = 5cos(t). This is our second parametric equation.

In conclusion, she set of parametric equations consists of x = 5sin(t) and y = 5cos(t).

NOTE: The direction of movement along the curve is clockwise. Convince yourself of this by graphing the set of parametric equations in desmos.com! For example, for the first set, you would input (5 sin(t), 5 cos(t) ). Then replace t with increasingly larger positive numbers and watch the curve develop in clockwise direction.

Example 6:

Find a set of parametric equations for the circle x² + y² = 25 again, but this time let .

Step 1:

Change the equation to standard form. Let's first divide both sides by 25 and reduce to get

This can be written as.

Step 2:

We will now use the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1.

We are given . But we can also see this by relating the Pythagorean Identity to the standard form in Step 1.

Expressed in terms of x, this is y = 5sin(t). This is our first parametric equation.

It follows that .

Expressed in terms of y, this is x = 5cos(t). This is our second parametric equation.

In conclusion, she set of parametric equations consists of x = 5cos(t) and y = 5sin(t).

NOTE: The direction of movement along the curve is counter-clockwise. Convince yourself of this by graphing the set of parametric equations in desmos.com! For example, for the first set, you would input (5 cos(t), 5 sin(t) ). Then replace t with increasingly larger positive numbers and watch the curve develop in counter-clockwise direction.

Example 7:

Find an equation in x and y given the set of parametric equations and . Let t consist of all real numbers.

Step 1:

Solve for t in one of the equations.

Let's use then .

Step 2:

Substitute 2y for t in the second equation and simplify.

We find

or

From our study of conic sections we know that this is the standard equation of a parabola open to the right with vertex at the origin!

Example 8:

Find an equation in x and y given the set of parametric equations x = 3cos(t) and y = 4sin(t).Let t be between 0 and .

Here we are presented with parametric equations containing sines and cosines. Therefore, we will use the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1.

Step 1:

We will isolate the trigonometric ratios in the given parametric equations as follows:

and

Step 2:

Replace cos(t) and sin(t) in the Pythagorean Identity sin²(t) + cos²(t) = 1 which is [sin(t)]² + [cos(t)] = 1 as follows:

or since mathematicians want to see x-terms first in an equation!

From our study of conic sections we know that this is the standard equation of an ellipse since a b. Its center is at the origin.

This equation can also be written as if we multiply both sides by 144.