TRIGONOMETRIC RATIOS OF ACUTE ANGLES
Example 1:
Find the value of sin 34o with the calculator rounded to four decimal places. The calculator must be in degree mode!
Input: sin(34) ENTER
NOTE: Left parenthesis will open when we activate the trigonometric function buttons on the calculator. After we type in the angle also called the argument, we MUST type in the right parenthesis, namely ")", before we press ENTER.
sin 34o
0.5592
Please note that the value of sin 34o is an irrational number. That is, it has an infinite number of decimal places!
Example 2:
Find the value of cos 75o with the calculator rounded to four decimal places. The calculator must be in degree mode!
Input: cos(75) ENTER
cos 75o
0.2588
Please note that the value of cos 75o is an irrational number. That is, it has an infinite number of decimal places!
Example 3:
Find the value of tan 84o with the calculator rounded to four decimal places. The calculator must be in degree mode!
Input: tan(84) ENTER
NOTE: Left parenthesis will open when we activate the trigonometric function buttons on the calculator. After we type in the angle also called the argument, we MUST type in the right parenthesis, namely ")", before we press ENTER.
tan 84o
Please note that the value of tan 84o is an irrational number. That is, it has an infinite number of decimal places!9.5144
Example 4:
Find the value of csc 39o with the calculator rounded to three decimal places.
Calculators only have a sin, cos, and tan key. Therefore, we MUST know and use the Reciprocal Identity
.
We also must make sure that the calculator is in degree mode.
Input: 1
sin(39) ENTER
csc 39o
1.589
Please note that the value of csc 39o is an irrational number. That is, it has an infinite number of decimal places!
Example 5:
Find the value of sec 13o with the calculator rounded to three decimal places.
We MUST use the Reciprocal Identity.
We also must make sure that the calculator is in degree mode.
Input: 1
cos(13) ENTER
sec 13o
1.026
Please note that the value of sec 13o is an irrational number. That is, it has an infinite number of decimal places!
Example 6:
Find the value of cot 64o with the calculator rounded to three decimal places.
We can use the Reciprocal Identity
or the Quotient Identity
.
NOTE: When working with the calculator, it is always best to use the Quotient Identity when evaluating cotangent. Sometimes, the calculator gives incorrect results when the Reciprocal Identity is used.
We must make sure that the calculator is in degree mode.
Input: cos(64)
sin(64) ENTER
cot 64o
0.488
Please note that the value of cot 64o is an irrational number. That is, it has an infinite number of decimal places!
Example 7:
Use the calculator to find the value of tan 1 rounded to 3 decimal places.
Since there is no degree symbol attached to the angle, the calculator must be in radian mode! Please note that radians are not always expressed in terms of
.
Input: tan(1) ENTER
tan 1
1.557
Please note that the value of tan 1 is an irrational number. That is, it has an infinite number of decimal places!
Example 8:
Use the calculator to find the value of
rounded to three decimal places.
Since there is no degree symbol attached to the angle, the calculator must be in radian mode!
Input: cos(
8) ENTER
NOTE: Always use the
symbol on the calculator and not 3.14.
Please note that the value of
is an irrational number. That is, it has an infinite number of decimal places!
Example 9:
Use the calculator to find the value of sec 1.4 rounded to three decimal places.
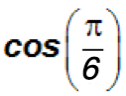 . Use a calculuator to find it.
. Use a calculuator to find it. 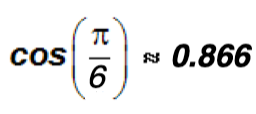 and we memorized that
and we memorized that