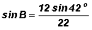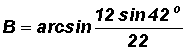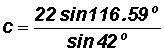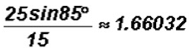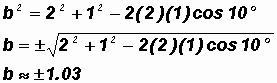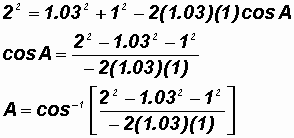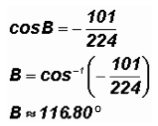THE LAWS OF SINES AND COSINES
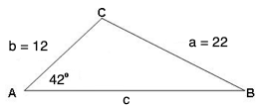
Example 1:For the oblique triangle with measures a = 22 in, b = 12 in, and A = 42o, find the remaining sides and angles. Round all calculations to two decimal places.
Assume angles A, B, and C are opposite sides labeled a, b, and c respectively.
HINT: Make a sketch!!!
Given two sides and one angle opposite one of the sides, we can use the Law of Sines
.
Solve for Angle B:
Specifically, we'll write
22 sin B = 12 sin 42o
Please note that sin B is positive. We know that the value of sine is positive for QI and QII angles!
NOTE: Since the sum of interior angles in a triangle is 180o and QI and QII angles are less than 180o, we could get two solutions for angle B, one acute and one obtuse angle.
Using the calculator, we find
Then, the QI angle is B1
21.41o.
Since B1 is also the reference angle, we find the second-quadrant angle to be
B2
180o
21.41o = 158.59o
Both of these angles could be solutions for the given triangle! As long as angle C is not negative, we will have a triangle with two solution sets.
Solve for Angle C:
We know that A = 42o, B1
21.41o, and B2
158.59o.
This is NOT a solution, since a triangle has NO negative interior angles. Thus,
is also NOT a solution.
We have just proven that this particular triangle only has ONE solution set!
Solve for Side c:
Given C
116.59o , let's find side c using the Law of Sines since we have two sides and one opposite angle:
DO NOT CALCULATE the individual values of the trigonometric ratios, instead use the EXACT value as shown below.
c
29.40 in
The triangle has the following solutions:
Given A = 42o, a = 22 in, and b = 21 in,
we found B
21.41o, C
116.59o, and c
29.40 in
Example 2:
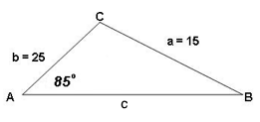
For the oblique triangle with measures a = 15 inches, b = 25 inches, and A = 85o, find the remaining sides and angles. Round all calculations to two decimal places.
Assume angles A, B, and C are opposite sides labeled a, b, and c respectively.
HINT: Make a sketch!!!
Given two sides and one angle opposite one of the sides, we can use the Law of Sines
.
Solve for Angle B:
Specifically, we'll write
15 sin B = 25 sin 85o
Please note that sin B is positive. We know that the value of sine is positive for QI and QII angles!
NOTE: Since the sum of interior angles in a triangle is 180o and QI and QII angles are less than 180o, we could get two solutions for angle B, one acute and one obtuse angle.
Using the calculator, we find
But the calculator tells us "Domain Error".
Investigating, we find
The result shows that sin B is greater than 1. However, the value of sin B oscillates only between
1 and 1.
Therefore, we must conclude that the triangle with the given measurements has NO solutions.
Below is a more accurate picture of the given information:
Example 3:
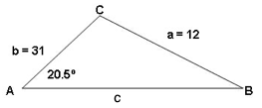
Example 4:For the oblique triangle with measures a = 12 ft, b = 31 ft, and A = 20.5o, find the remaining sides and angles. Round all calculations to two decimal places.
Assume angles A, B, and C are opposite sides labeled a, b, and c respectively.
HINT: Make a sketch!!!
Given two sides and one angle opposite one of the sides, we can use the Law of Sines
.
Solve for Angle B:
Specifically, we'll write
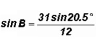
12 sin B = 31 sin 20.5o
Please note that sin B is positive. We know that the value of sine is positive for QI and QII angles!
NOTE: Since the sum of interior angles in a triangle is 180o and QI and QII angles are less than 180o, we could get two solutions for angle B, one acute and one obtuse angle.
Using the calculator, we find
Then, the QI angle is B1
64.78o.
Since B1 is also the reference angle, we find the QII angle to be
B2
180o
64.78o = 115.22o
Both of these angles could be solutions for the given triangle! As long as angle C is not negative, we will have a triangle with two solution sets.
Solve for Angle C:
We know that A = 20.5o, B1
64.78o, and B2
115.22o.
Then
and
Since both measures for angle C are positive the triangle indeed has TWO solution sets.
Solve for Side c:
Given
, let's find side
using the Law of Sines since we have two sides and one opposite angle:
12 sin 94.72o = c1 sin 20.5o
DO NOT CALCULATE the individual values of the trigonometric ratios, instead use the EXACT value as shown below.
Given
, let's find side
by using the Law of Sines.
12 sin 44.28o = c2 sin 20.5o
DO NOT CALCULATE the individual values of the trigonometric ratios, instead use the EXACT value as shown below.
The triangle has the following solutions:
Given A = 20.5o, a = 12 ft, and b = 31 ft,
we found B1
64.78o, C1
94.72o, and c1
34.15 ft
or B2
115.22o, C2
44.28o, and c2
23.92 ft
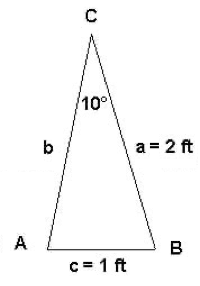
Solve the oblique triangle pictured below. Round all calculations to two decimal places.
Given two sides and one angle opposite one of the sides, we could use the Law of Sines. However, let's instead use the Law of Cosines to show that this law can be used as well.
Solve for Side b:
Let's use
.
Note that the radicand was not changed to a decimal approximation before taking its square root! It is better to keep the numbers as exact as possible for as long as possible.
Disregarding the negative value above (distances are never negative!!!), we get
b
1.03 ft
Solve for Angle A:
Let's use
using the UNROUNDED value for Side b.
Please note that the fraction above was not turned into a decimal approximation. It was typed into the calculator using appropriate grouping symbols to keep the solution as exact as possible.
A
160.27o
There cannot be another angle because the only other quadrant in which cos A is negative is Q III, where the angles are greater than 180o.
Solve for Angle B:
We know that A
160.27o and C = 10o.
Let's use the fact that the sum of interior angles in a triangle is 180o.
B
180o
160.27o
10o = 9.73o
The triangle has the following solutions:
Given a = 2 ft, c = 1 ft, and 10o,
we found A
160.27o, B
9.73o, and b
1.03 ft
Example 5:
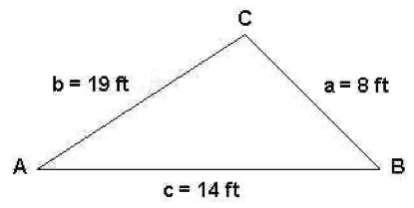
Solve the following oblique triangle. Round all calculations to two decimal places.
Let's use the Law of Cosines because we do not have at least one side and its opposite angle which is necessary to use the Law of Sines.
Solve for Angle A:
Use
.
Note that 493/532 was not changed to a decimal approximation in the interest of more exact solutions.
There cannot be another solution because the only other quadrant in which cosine is positive is QIV, but there the angles are greater than 180o.
Solve for Angle B:
We'll use the Law of Cosines again. Specifically, we will use
.
Note that
101/224 was not turned into a decimal approximation!
Solve for Angle C:
We know that A
22.5o and B
116.80o
Let's use the fact that the sum of interior angles in a triangle is 180o.
C
180o
22.08o
116.8o = 41.12o
The triangle has the following solutions:
Given a = 8 ft, b = 19 ft, and c = 14 ft,
we found A
22.08o, B
116.8o, and C
41.12o