INVERSE TRIGONOMETRIC FUNCTIONS

Example 1:

Using a calculator, find sin ^-1(0.86) in degrees and radians rounded to two decimal places. 

You access sin ^-1 by first pressing the "2nd" or "Shift" key on your calculator and then pressing the "sin" key.

If you want your angles to be in radians, make sure your calculator is in "Radian Mode".  If you want your angles to be in degrees, your calculator must be in "Degree Mode."

This calculation will result in approximately 59.32^o or 1.04 radians.

Example 2:

Using a calculator, find cos ^-1(0.87) in degrees and radians rounded to two decimal places.

You access cos ^-1 by first pressing the "2nd" or "Shift" key on your calculator and then pressing the "cos" key. 

This calculation results in approximately 29.54^o or 0.52 radians.

Example 3:

Using a calculator, find tan ^-1(0.59) in degrees and radians rounded to two decimal places. 

You access tan ^-1 by first pressing the "2nd" or "Shift" key on your calculator and then pressing the "tan" key. 

This calculation results in approximately 30.54^o or 0.53 radians

Example 4:

Compare some trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

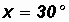
Given let Then

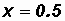
Given let Then

Please note that arcsin(0.5) gives us back an angle of 30^o.

Example 5:

Compare some trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

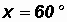
Given let Then

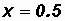
Given let Then

Please note that arccos(0.5) gives us back an angle of 60^o.

Example 6:

Compare some trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

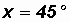
Given let Then

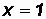
Given let Then

Please note that arctan(1) gives us back an angle of 45^o.

Example 7:

Let's compare some more trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

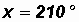
Given let Then

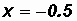
Given let Then

Please note that arcsin(0.5) DOES NOT gives us back an angle of 210^o.

WHY? 

Due to the range restrictions for the inverse sine function to 90^o y 90^o, the calculator gives us the angle from the restricted range. That's why the arcsin(0.5) is 30^o and not 210^o.

Example 8:

Compare some trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

Given let Then

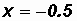
Given let Then

Please note that arccos(0.5) DOES NOT gives us back an angle of 240^o.

WHY? 

Due to the range restrictions for the inverse cosine function to 0^o y 180^o, the calculator gives us the angle from the restricted range. That's why the arccos(0.5) is 120^o and not 240^o.

Example 9:

Compare some trigonometric functions with their inverses.  KEEP YOUR CALCULATOR IN DEGREE MODE!

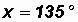
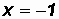
Given let Then	Given let Then

Please note that arctan(1) DOES NOT gives us back an angle of 135^o.

WHY? 

Due to the range restrictions for the inverse tangent function to 90^o < y < 90^o, the calculator gives us the angle from the restricted range. That's why the arctan(1) is 45^o and not 135^o.