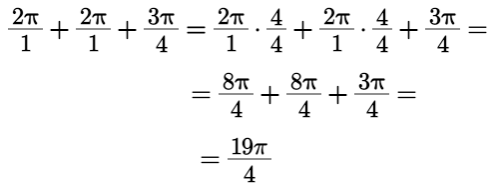INTRODUCTION TO ANGLES

Example 1:

Which angles are integer multiples of special angles?

Special angles are 30^o, 45^o, and 60^o.

a. 388^o

not a multiple of special angle since neither 30, nor 45, nor 60 divides into angle evenly

b. 330^o

11(30^o), multiple of special angle

c. 225^o

5(45^o), multiple of special angle

d. 119^o

not a multiple of special angle since neither 30, nor 45, nor 60 divides into angle evenly

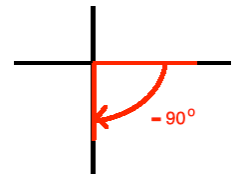
e. 120^o NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

2(60^o), multiple of special angle

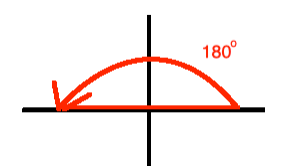
f. 150^o NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

5(30^o), multiple of special angle

Example 2:

Which angles are integer multiples of special angles? Sometimes it is easier to change the angles to degrees before you decide!

Special angles are and and .

a. /8

22.5^o, not a special angle

b. 5/3

5/3 560^o, multiple of special angle

c. 3/4

3/4 345^o, multiple of special angle

d. /5

36^o, not a special angle

e. 7/6

7/6 730^o, multiple of special angle

f. 4/9

80^o, not a special angle

Example 3:

Which angles are quadrantal angles?

Remember, ALL quadrantal angles are integer multiples of 90^o!

a. 388^o

4(90^o) + 28^o , QI angle

b. 450^o

5(90^o), quadrantal angle

c. 720^o

8(90^o), quadrantal angle

d. 390^o

4(90^o) + 30^o, QIII angle

e. 540^o NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

6(90^o), quadrantal angle

f. 225^o NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

2(90^o) 45^o, QII angle

Example 4:

Which angles are quadrantal angles? Sometimes it is easier to change the angles to degrees before you decide!

Remember, ALL quadrantal angles are integer multiples of !

a. /8

22.5^o, QI angle

b. 5/2 NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

5/2 590^o, quadrantal angle

c. 3/2

3/2 390^o, quadrantal angle

d. 6/5

216^o, QIII angle

e. NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

2/2 290^o, quadrantal angle

Example 5:

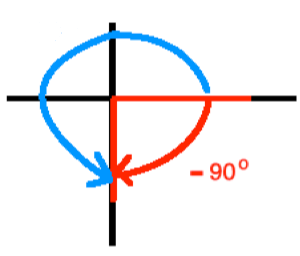
a. Graph the quadrantal angle 90^o.

b. Find the smallest positive angle in degrees that is coterminal to 90^o.

It is best to graph this situation.

We quickly see that the angle with measure 270^o is the smallest positive angle that is coterminal with 90^o.

c. Find the smallest negative angle in degrees that is coterminal to 90^o.

Please note that a negative sign simply indicates clockwise direction!

We quickly see that the angle with measure 90^o + 360^o = 450^o is the smallest negative angle that is coterminal with 90^o.

Example 6:

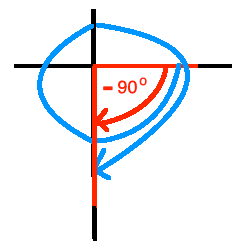
a. Graph the quadrantal angle 180^o.

b. Find the smallest positive angle in degrees that is coterminal with 180^o.

It is best to graph this situation.

We quickly see that the angle with measure 180^o + 360^o = 540^o is the smallest positive angle that is coterminal with 180^o.

c. Find the smallest negative angle in degrees that is coterminal with 180^o.

Please note that a negative sign simply indicates clockwise direction!

We quickly see that the angle with measure 180^o is the smallest negative angle that is coterminal with 180^o.

Example 7:

Find all angles that are coterminal with a 5/3 angle.

We can find angles that are coterminal to it by ADDING integer multiples of 2. We will name the integer k to express ALL angles coterminal to 5/3 as follows:

5/3 + 2k, where k is any integer

For instance,

when k = 2, then 5/3 + 2(2) = 5/3 + 4

                                                  = 5/3 + 12/3 (need common denominator)

                                                  = 17/3

when k = 1, then 5/3 + 2(1) = 5/3 + 2

                                                  = 5/3 + 6/3 (need common denominator)

                                                  = 11/3

when k = 1, then 5/3 + 2(1) = 5/3 2

                                                        = 5/3 6/3 (need common denominator)

                                                        = /3

when k = 2, then 5/3 + 2(2) = 5/3 4

                                                        = 5/3 12/3 (need common denominator)

                                                        = 7/3

Example 8:

Find an angle between 0 and 2 that is coterminal with the angle 11/2.

We can find an angle that is coterminal to 11/2 by SUBTRACTING from it integer multiples of 2 until the difference is smaller than 2. This difference is a coterminal angle.

11/2 = 8/2 + 3/2

           = 4 + 3/2

           = 2 + 2 + 3/2

We find that 3/2 is coterminal with 11/2.

Example 9:

Find an angle between 0^o and 360^o that is coterminal with the angle 1290^o.

We can find an angle that is coterminal to 1290^o by SUBTRACTING from it integer multiples of 360^o until the difference is smaller than 360^o. This difference is a coterminal angle.

1290^o = 360^o(3) + 210^o.

We find that the angle 210^o is between 0^o and 360^o and is coterminal with the 1290^o angle.

Example 10:

Find the location of the terminal side of the following angles. NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

Hint: Graph them!

*********************************************************************************************

a.      77o - Quadrant I angle	b.     77o - Quadrant IV angle
c.   125o  - Quadrant II angle	d.   125o - Quadrant III angle
e.   216o  - Quadrant III angle	f.    216o - Quadrant II angle
g.   330o - Quadrant IV angle i.   960o = 360o(2) + 240o     Quadrant III angle using the angle 240o     which is coterminal to the angle 960o	h.   330o - Quadrant I angle   j.   376o = 360o(1) + (16o)       Quadrant IV angle using the angle 16o       which is coterminal to the angle 376o

Example 11:

Find the location of the terminal side of the following angles. NOTE: The negative sign only indicates that we must draw the arc of the angle in clockwise directions.

Hint: If necessary, convert the angles to degrees, then graph them.

*********************************************************************************************

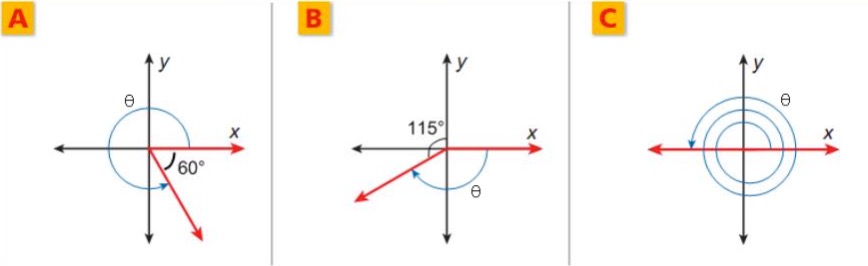
Find the angle measures from each graph.

A.

= 360^o 60^o = 300^o

B.

Here we must first find the angle between the terminal side of angle and the negative x-axis. Given is 115^o. We can change it to the sum of 90^o and 25^o. Therefore, tha angle between the terminal side of and the negative x-axis is 25^o.

Then = 180^o +25^o = 155^o

C.

We see that angle has two full rotations, which equals 360^o(2). Remaining is a rotation of

180^o.

Then = 360^o(2) +180^o = 900^o

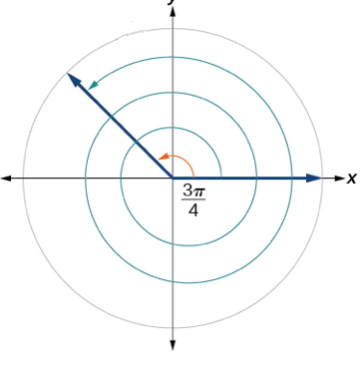
Example 13:

Find the measure of the angle below in radians. Express the angle as an improper fraction in terms of . HINT: You can always convert to degrees to make calculations easier!

The direction of the angle is counter-clockwise. Therefore, we are dealing with a positive angle. We are counting two full rotations which is 2 + 2 = 4. To it we will add the measure of the arc .

We are supposed to express the answer as an improper fraction in terms of . When adding fractions, we need a common denominator. In our case, it is 4.

The measure of the angle in radians is .