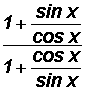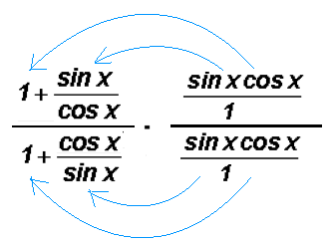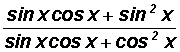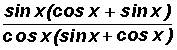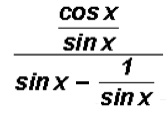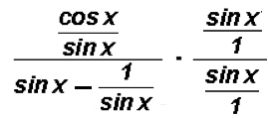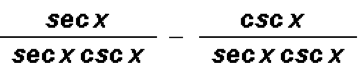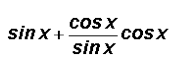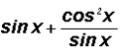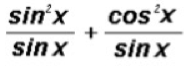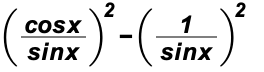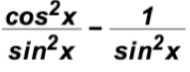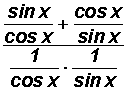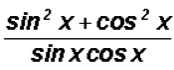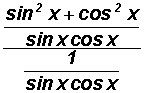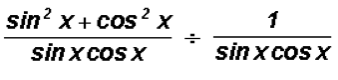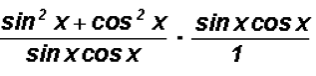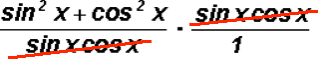SIMPLIFYING TRIGONOMETRIC EXPRESSIONS - PART 2

In the following examples, we will apply one or more of the six most common methods used to simplify trigonometric expressions.

Please note that a trigonometric expression can often be simplified using several different approaches. The methods shown here work well for the instructor. Your brain may be wired differently, and you might use another approach to simplify.

By the way, for a beginner simplifying trigonometric expressions is usually not easy. It is often fractions that give trouble. You will have to work many, many simplification problems before the process becomes easier.

1. Use fundamental identities to rewrite trigonometric ratios and expressions.

2. Add or subtract trigonometric ratios. Know how to work with fractions!

3. Multiply trigonometric ratios and expressions.

4. Factor trigonometric expressions.

5. Separate fractions into two or more fractions.

6. Change complex fractions to simple fractions.

Example 1:

The expression can be reduced to a single trigonometric ratio.  Find this ratio.

We will cancel out the expression since it occurs both in the numerator and the denominator.

We are left with .

We can now use a Reciprocal Identity.

That is, we can state that equals sec x.

Example 2:

The expression can be reduced to a single trigonometric ratio, such as cos(x), sin(x), tan(x), sec(x), csc(x), or cot(x).  Find this ratio.

What could we do?

Let's use fundamental identities to rewrite the trigonometric ratios.

NOTE:  While this is certainly a good start, it does not guarantee success.  We might have to give up and think of something else to do!

We can use Quotient Identities to write tangent and cotangent as follows:

Now what?

Let's change the complex fraction to a simple fraction using the method that requires us to multiply by a special form of the number 1.

This will be comprised of as illustrated below.

The arrows indicate how the terms of the second fraction must be distributed to the first fraction. After multiplying and reducing we will end up with a simple fraction. Please investigate in detail. This is nothing but 5th grade fraction concepts using trigonometric ratios instead of numbers.

Now what?

Let's factor common factors out of the numerator and the denominator.

As you can see, the numerator and denominator have a factor in common and when reduced we end up with

. 

Now what?

Let's use a fundamental identity to rewrite the trigonometric expression.

Given the Quotient Identity , we can write as tan x.

We have shown that can be reduced to the single trigonometric ratio tan x.

Example 3:

The expressioncan be reduced to the negative of a single trigonometric ratio, such as cos(x), sin(x), tan(x), sec(x), csc(x), or cot(x).  Find this ratio.

What could we do?

Let's use fundamental identities to rewrite some of the trigonometric ratios.

NOTE:  While this is certainly a good start, it does not guarantee success.  We might have to give up and think of something else to do!

We can use Reciprocal and Quotient Identities to write cotangent and cosecant as follows:

Now what?

Let's change the complex fraction to a simple fraction using the method that requires us to multiply by a special form of the number 1.

This will be comprised of sin x as illustrated below.

After multiplying and reducing we will end up with a simple fraction. Please investigate in detail. This is nothing but 5th grade fraction concepts using trigonometric ratios instead of numbers.

Now what?

The expression should remind us of a Pythagorean Identity, namely . But in our case, the signs are "not quite right."

Let's multiply this Pythagorean Identity by 1.

1 ()

Now we can state that

equals

As we can see, the numerator and denominator have a factor in common and when reduced we end up with

Now what?

Let's use a fundamental identity to rewrite the expression.

Given the Reciprocal Identity , we can write as sec x.

We have shown thatcan be reduced to the negative of a single trigonometric ratio, namely sec x.

Example 4:

Reduce the trigonometric expression to a difference of two trigonometric ratios. 

What could we do?

Let's separate the fraction into two fractions.

NOTE:  While this is certainly a good start, it does not guarantee success.  We might have to give up and think of something else to do!

Now we can cancel the secants in the first term and the cosecants in the second term to get

Now what?

Let's use fundamental identities to rewrite the trigonometric expressions.

Using Reciprocal Identities, we find that equals sin x cos x.

We have shown that can be reduced to a difference of two trigonometric ratios, namely sin x cos x.

Example 5:

The expression sin x + cot x cos x can be reduced to a single trigonometric ratio, such as cos(x), sin(x), tan(x), sec(x), csc(x), or cot(x).  Find this ratio.

What could we do?

Let's use the fundamental identities to rewrite some of the ratios.

NOTE:  While this is certainly a good start, it does not guarantee success.  We might have to give up and think of something else to do!

We can use a Quotient Identity to rewrite cotangent as follows:

and then we multiply as follows:

Now what?

Let's add the trigonometric expressions.

Here we are dealing with a fraction. In order to add and subtract fractions, we learned in arithmetic that we must find a common denominator. That is, we usually find the smallest number that is divisible by both given denominators.

The smallest number divisible by both the denominators is sin x. We will multiply the numerator and denominator of the first term by sin x. The second term already has a denominator of sin x.

 

and

Now what?

Let's use fundamental identities to rewrite the expression.

Given the Pythagorean Identity , we can write as

.

Now what?

Let's use a fundamental identity to rewrite the expression.

Given the Reciprocal Identity , we can write as csc x.

We have shown that sin x + cot x cos x can be reduced to csc x.

Example 6:

The expression cot²x csc²x can be reduced to a single number.  Find this number.

What could we do?

Let's use fundamental identities to rewrite the ratios.

NOTE:  While this is certainly a good start, it does not guarantee success.  We might have to give up and think of something else to do!

We can use a Reciprocal and Quotient Identity to write cotangent and cosecant as follows:

and distributing the exponents we get

and

Now what?

The expression in the numerator should remind us of a Pythagorean Identity, namely. But in our case, the signs are "not quite right."

Let's multiply this Pythagorean Identity by 1.

1 ()

sin² = 1 + cos²

We see that cos² x 1 equals sin² x, therefore, we can write as

which equals 1.

We have shown that cot² x csc² x can be reduced to the single number 1.