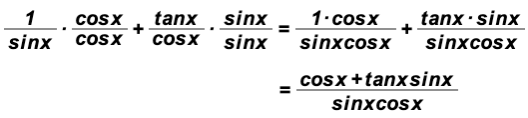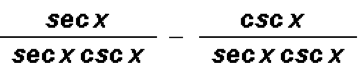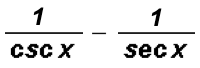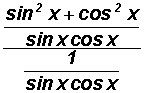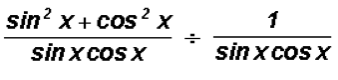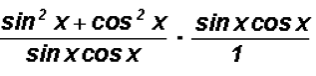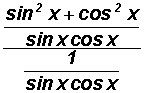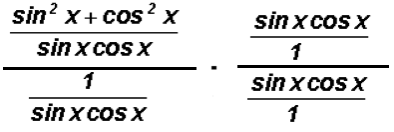SIMPLIFYING TRIGONOMETRIC EXPRESSIONS - PART 1

Example 1:

Use a Pythagorean Identity to rewrite the expression .

Given the Pythagorean Identity , we can rewriteas .

We can actually use exponential properties to rewrite as .

Example 2:

Add 5 sin x + 3 sin x

We add the coefficients of like ratios!

8 sin x

Example 3:

Add .

Here we are dealing with a fraction. In order to add and subtract fractions, we learned in arithmetic that we must find a common denominator. That is, we usually find the smallest number that is divisible by both given denominators.

Here it is .

To change all denominators to be the common denominator, we will multiply as follows:

Example 4:

Subtract 2 sec x 7 sec x

We subtract the coefficients of like ratios!

5 sec x

 Example 5:

Simplify

Example 6:

Carry out the following multiplication: (sin x + cos x)² .

(sin x + cos x)² = (sin x + cos x)(sin x + cos x)

Using FOIL, we get

sin² x + 2sin x cos x + cos² x

Example 7:

Multiply sin x (sin x + cos x)

Here we use the Distributive Property and the Laws of Exponents to find

sin² x + sin x cosx

Example 8:

Factor sin x cos x sin x.

We see that both terms have a common factor. It is sin x and we will factor it out of each term as follows:

sin x cos x sin x = sin x (cos x 1)

Example 9:

Factor sec² x 1.

Noticing that we are dealing with a Difference of Squares, we can write

sec² x 1 = (sec x 1)(sec x + 1)

Example 10:

Factor tan² x + 5tan x + 6.

The expression is actually "like" a trinomial which we used to factor in algebra. Let's make the following substitution:

Let a = tan x.

We can now write the given expression as a² + 5a + 6 which can be factored and written as

(a + 3)(a + 2).

Now we will let a equal tan x again and write (tan x + 3)(tan x + 2).

We find that tan² x + 5tan x + 6 can be factored and written as (tan x + 3)(tan x + 2).

Example 11:

Separate into two fractions then simplify.

Any time we have terms in the numerator separated by a minus or plus sign, we can assign to each term the entire denominator as follows:

Now we can cancel the secants in the first term and the cosecants in the second term to get

Example 12:

Change the following complex fraction to a simple fraction.

Let's take one of the fraction bars and write it as .

The complex fraction can then be changed to the following:

From arithmetic we know that dividing by a fraction is the same as multiplying by the reciprocal of the fraction. We will do this next.

Under multiplication, we can now cancel the numerator of the second fraction with the denominator of the first fraction.

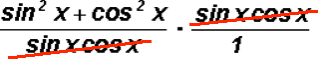
and we end up with which equals sin²x + cos²x.

Example 13:

We will change the complex fraction from Example 12 to a simple fraction again, but this time we will use a different method.

Let's multiply the complex fraction by a special form of the number 1.

It will be comprised of as illustrated below.

After canceling in the numerator of the complex fraction and in the denominator, we get

which equals sin²x + cos²x.