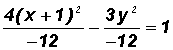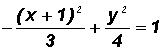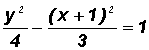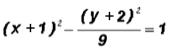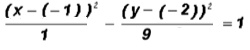CONIC SECTIONS: THE HYPERBOLA

Example 1:

Write the standard equation of the following hyperbola. Then find the coordinates of the center.

This equation is almost in standard form. Since there is a positive y²-term and a negative x²-term, we know that this hyperbola is of the form

. It is a hyperbola with a vertical transverse axis.

NOTE: The center (h, k) of this hyperbola is at (0, 0) because there is only a y²-term and an x²-term in the numerator. Therefore, we can write

where h = 0, k = 0, a = 5 (from denominator of positive term!), and b = 4

The coordinates of the center are (0, 0).

Example 2:

Write the standard form of the following equation of a hyperbola. Then find the coordinates of the center.

.

The hyperbola must be of the form or .

Let's divide both sides of the equation by 12 to get a 1 on the right side of the equal sign.

and

or

We can now write the standard equation of the given hyperbola as follows:

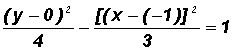
where h = 1, k = 0, a = 2 (from denominator of positive term!), and b =

This is a hyperbola with a vertical transverse axis.

The coordinates of the center are (1, 0).

Example 3:

rite the standard form of the following equation of a hyperbola. Then find the coordinates of the center.

This equation is almost in standard form. Since there is a positive y²-term and a negative x²-term, we know that this hyperbola is of the form. This is a hyperbola with a horizontal transverse axis.

All we have to do is give the x²-term a denominator of 1 and insert minus signs into both numerators as follows:

where h = 1, k = 2, a = 1 (from denominator of positive term!), and b = 3

Now, we can find the requested information as follows:

The coordinates of the center are (1, 2).