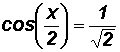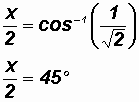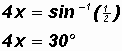SOLVING COMPLEX TRIGONOMETRIC EQUATIONS

Example 1:

Solve 2sin² x 3sin x + 1 = 0 for x on the interval . Express the solutions in degrees.

Step 1:

This equation is "quadratic" in form. That is, one variable (sin x) is raised to the second power and the other, same variable, is raised to the first power.

Nothing needs to be done because the equation only contains sine ratios.

Step 2:

We are going to use the Quadratic Formula to find one or more simple trigonometric equations. To make the solution process a little bit more palatable, let's use the following substitution. That is, we let sin x = k, then sin² x = k².

It follows that 2sin² x 3sin x + 1 = 0 becomes 2k² 3k + 1 = 0.

We are now going to use the Quadratic Formula , but our variable will be k instead of x.

For this procecure, we notice that a = 2, b = 3 and c = 1.

Then

and .

We find two solutions, namely and .

Since k is actually equal to sin x, we will back-substitute to get sin x = 1 and sin x =

We now have two simple trigonometric equations. We must try to find solutions for both.

Steps 3 through 6:

Let's find the solutions of the two simple trigonometric equations we would in Step 2.

We will use the calculator to solve sin x = .

Using the arcsine, we find x = 30^o, which indicates a reference angle of 30^o.

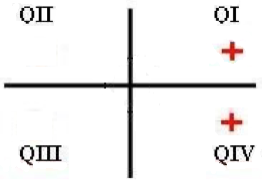
Next, we will use All Students Take Calculus to find the quadrants in which the sine ratio is positive.

We need to find angles located in QI and QII that have a reference angle of 30^o. We find the solutions for angle x on the interval to be as follows:

Solution in QI:

x₁ = 30^o

Solution in QII:

x₂ = 180^o30^o = 150^o

We will use the calculator to solve sin x = 1.

With the calculator in degrees and using the arcsine, we find x = 90^o, which indicates a Quadrantal Angle, therefore, there is no reference angle.

Next, we use the following picture:

We find one solution for angle x on the interval to be 90^o.

In summary, the solutions of 2sin² x 3sin x + 1 = 0 on the interval are 30^o, 90^o, and 150^o.

Example 2:

Solve sin²x 2cos x 2 = 0 for x on the interval . Express the solutions in degrees.

Step 1:

This equation is "quadratic" in form. However, it contains sine and cosine ratios. We must change the equation so that it contains either all cosines or all sines.

Remembering the Pythagorean Identity sin²x = 1 cos² x, we can change the given equation to the following:

(1 cos² x) 2cos x 2 = 0

Writing in descending powers of cos x:

cos² x 2cos x 1 = 0

Finally, we will multiply both sides by 1 to get cos² x + 2cos x + 1 = 0.

Step 2:

We are going to use the Quadratic Formula to find one or more simple trigonometric equations. To make the solution process a little bit more palatable, let's use the following substitution. That is, we let cos x = k, then cos² x = k².

It follows that cos² x + 2cos x + 1 = 0 becomes k² + 2k + 1 = 0.

We are now going to use the Quadratic Formula , but our variable will be k instead of x.

For this procecure, we notice that a = 1, b = 2 and c = 1.

Then

and .

We find one solution, namely k = 1.

Since k is actually equal to cos x, we will back-substitute to get cos x = 1. and find its solutions.

Steps 3 through 6:

Let's find the solutions of the two simple trigonometric equations we would in Step 2.

We will use the calculator to solve cos x = 1.

With the calculator in degrees and using the arccosine, we find x = 180^o, which indicates a Quadrantal Angle, therefore, there is no reference angle.

Next, we use the following picture:

In summary, there is only one solution of sin²x 2cos x 2 = 0 on the interval , namely x = 180^o.

Example 3:

Solve 4 sin² x cot x cot x = 0 for x on the interval .  Express the solutions in radians.

Step 1:

This equation contains sine and cotangent ratios with one of the cotangent ratios being connected to the squared sine ratio via multiplication. Therefore, we will NOT attempt to change the equation so that it contains either all sines or all cotangents.

Step 2:

Trying to find one or more simple trigonometric equations using theQuadratic Formula would be nearly impossible. Luckily, we notice that cot x is the greatest common factor between the two terms. Therefore, we will start by factoring it out.

4 sin² x cot x cot x = 0

cot x (4 sin² x 1) = 0

Now we will use the Zero Product Principle which allows us to set both factors equal to 0. We will get two equations.

(1) cot x = 0

This is a simple trigonommetric equation. We will solve it in Steps 3 through 6 below.

(2) 4 sin² x 1 = 0

This is still a quadratic equation. We could use the Quadratic Formula to solve it. However, we know from algebra that we can use a short-cut method called the Square Root Property when the equation only contains a squared variable.

First, we will isolate the squared term on one side of the equal sign to get . Note that the coefficient of the squared term must be 1!

Then we will take the square root of oth sides to get. Here, we actually have two equations, namely sin x = and sin x = .

We now have three simple trigonometric equations. We must try to find solutions for all of them.

Steps 3 through 6:

Let's find the solutions of the three simple trigonometric equations we would in Step 2.

Finding the angle x for cot x = 0 with the calculator is cumbersome.

Hopefully, we remember that the cotangent ratio is only 0 when the angle is quadrantal. We also hopefully remember that .

The sine ratio cannot equal 0 otherwise the cotangent ratio is undefined. Let's look at the following picture.

At which angles is the sine ratio NOT equal to 0? We find two solution for angle x on the interval , namely /2 and 3/2.

We will use the calculator to solve sin x = and sin x = .

With the calculator in degrees and using the arcsine, we find x = 30^o and x = 30^o, which indicates a reference angle of 30^o in both cases.

Next, we will use All Students Take Calculus to find the quadrants in which the sine ratio is positive. Therefore, the sine in negative in QIII and QIV.

 

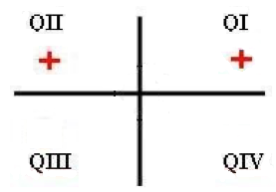
We need to find angles located in QI, QII, QIII, and QIV that have a reference angle of 30^o. We find the solutions for angle x on the interval to be as follows:

Solution in QI:

x₁ = 30^o /6

Solution in QII:

x₂ = 180^o 30^o = 150^o 5/6

Solution in QIII:

x₂ = 180^o + 30^o = 210^o 7/6

Solution in QIV:

x₂ = 360^o 30^o = 330^o 11/6

In summary, the solutions of cot x = 4 sin² x cot x on the interval are

/2, 3/2, /6 , 5/6, 7/6, and 11/6.

Example 4:

Solve for x on the interval .  Express the solutions in degrees.

Step 1:

This equation is "quadratic" in form. However, it only contains a squared cosine ratio.

Step 2:

We will try to find simple trigonometric equations by using the Square Root Property instead of the Quadratic Formula.

First, we must change the leading coefficient of the square trigonometric term to 1 by dividing both sides of the equation by 2.

We can now apply the Square Root Property to . Subsequently we get

We now have two simple trigonometric equations, namely

and

We must try to find solutions for both.

Steps 3 through 6:

Let's find the solutions of the two simple trigonometric equations we would in Step 2.

We will use the calculator to solve and .

With the calculator in degrees and using the arccosine, we find x = 45^o and x = 135^o, which indicates a reference angle of 45^o in both cases.

Next, we will use All Students Take Calculus to find the quadrants in which the cosine ratio is positive. Therefore, the cosine is negative in QII and QIII.

   and       

We need to find angles located in QI, QII, QIII, and QIV that have a reference angle of 45^o. We find the solutions for the angle x on the interval to be as follows:

Solution in QI:

x₁ = 45^o

Solution in QII:

x₂ = 180^o 45^o = 135^o

Solution in QIII:

x₃ = 180^o + 45^o = 225^o

Solution in QIV:

x₄ = 360^o 45^o = 315^o

In summary, the solutions of on the interval are 45^o, 135^o, 225^o, and 315^o.

Example 5:

Solve for x on the interval .  Express the solutions in degrees.

Here we we have an equation were bx = which is the same as x.

Please note that we will work with the angle through Step 5. Only in Step 6 will we find the solution(s) for angle x.

Step 1:

The solution interval for angle x is .

The solution interval for angle is half of this, namely . 

Steps 2 through 5:

Isolate the trigonometric expression on one side:

We are going to use the concept of Inverse Trigonometric Functions to solve for the angle using the calculator in degree mode.

Please note that you cannot at this point multiply both sides of the equation by 2 to get a solution for angle x!!!

The reference angle for angle equals 45^o.

The value of the cosine ratio in (2) is positive and we have a reference angle.

We will use All Students Take Calculus to find the quadrants in which the cosine ratio is positive. It is best to draw a picture!

Finally, we are going to use the reference angle from Step 3.  We need to find angles located in QI and QIV that have a reference angle of 45^o. 

Therefore, the solutions for angle on the interval are as follows:

= 45^o

and = 360^o45^o = 315^o

Step 6:

Since we are asked to solve for angle x, we must now multiply both sides of the above equations by 2 to get

In summary, the solutions of on the interval are 90^o and 630^o.

Example 6:

Solve for x on the interval .  Express the solutions in EXACT radians.

Here we we have an equation were bx = 4x.

Please note that we will work with the angle 4x through Step 5. Only in Step 6 will we find the solution(s) for angle x.

Step 1:

The solution interval for angle x is .

The solution interval for angle 4x is four times as large as this, namely . 

Steps 2 through 5:

Isolate the trigonometric expression on one side:

We are going to use the concept of Inverse Trigonometric Functions to solve for the angle 4x using the calculator. 

Let's work with degrees! Using the calculator in degree mode, we find

Please note that you cannot at this point divide both sides of the equation by 4 !!!

The reference angle of angle 4x equals 30^o.

The value of the sine ratio in (2) is positive and we have a reference angle.

Qe will use All Students Take Calculus to find the quadrants in which the sine ratio is positive. It is best to draw a picture!

Finally, we are going to use the reference angle from Step 3.  Now, remember the solution interval for angle 4x is in degrees.

However, we are going to find angles in the solution interval first. They must be in QI and QII and have a reference angle of 30^o. 

They are

4x₁ = 30^o

4x₂ = 180^o 30^o = 150^o

Since we are supposed to find solutions for angle 4x on the interval , we must add the following angles, which are coterminal to the two we already found:

4x₃ = 30^o + 360^o = 390^o

4x₄ = 150^o + 360^o = 510^o

Let's go ahead and express these four solutions in radians as follows:

                                                       

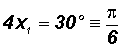
Step 6:

Since we are asked to solve for the angle x, we must now divide both sides of the above equations by 4 to get

                           

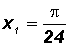
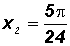
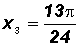
In summary, the solutions of on the interval are

                            .
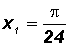
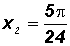
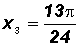