SOLVING SIMPLE TRIGONOMETRIC EQUATIONS
Example 1:
Solve
for x in the interval
. Express the solutions in EXACT radians.
Step 1:
The solution interval for angle x is
. The trigonometric ratio is already isolated on one side of the equal sign.
Therfore, we use
.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x i the equation from Step 1 using the calculator.
Given
, we find x = tan -1 (
)
Helpful Hint: It is often easier to work in degrees and then change the solutions back to radians. So let's change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x = 60o
Step 3:
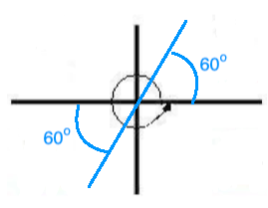
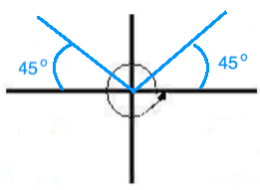
Given a solution for angle x in Step 2, we will find its reference angle. Since angle 60o is a QI angle, its reference angle equals 60o.
Step 4:
We have a reference angle and the value of the tangent ratio in Step 1 is positive.
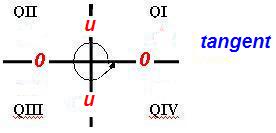
Therefore, we will use All Students Take Calculus to find the quadrants in which the tangent ratio is positive. See picture below!
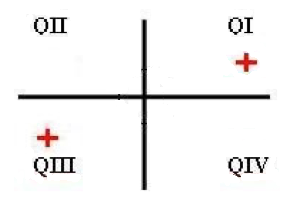
Finally, let’s first indicate the solution interval for angle x by graphing the angle 360o. Then we draw the reference angle in the appropriate quadrants.
We can now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QI:
x1 = 60o
Solution in QIII:
x2 = 180o + 60o = 240o
Since we are supposed to express the solutions in terms of radians we get
x1 =
/3
and x2 = 4
/3
Example 2:
Find the general solution of
for x. Express it in EXACT radians.
Whenever we are asked to find generalsolutions, we first find the solutions in the interval
. We already did this in Example 1.
We found x1 =
/3 (
60o) and x2 = 4
/3 (
240o).
We note that these two solutions are exactly
(
180o) apart. Therefore, we will only add
k the smallest solution.
That is, the general solution of
is
/3 +
k.
Example 3:
We are going to solve
again, but now we only want solutions for x in the interval
. Express the solutions in EXACT radians. Compare with Example 1!
Step 1:
The solution interval for angle x is
. The trigonometric ratio is already isolated on one side of the equal sign.
Therefore, we use
.
Step 2:
Given
, we find x = tan -1 (
)
Helpful Hint: It is often easier to work in degrees and then change the solutions back to radians. So lrt's change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x = 60o
Step 3:
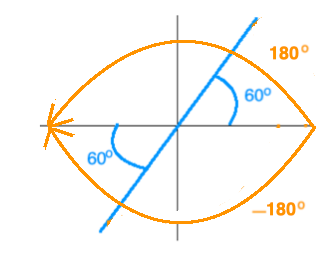
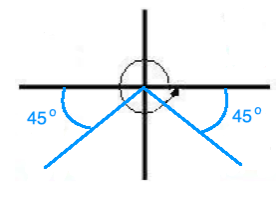
Given a solution for angle x in Step 2, we will find its reference angle. Since angle 60o is a QI angle, its reference angle equals 60o.
Step 4:
We have a reference angle and the value of the tangent ratio in Step 1 is positive.
Therefore, we will use All Students Take Calculus to find the quadrants in which the tangent ratio is positive. See picture below!

Finally, let's first indicat the solution intervale for angle x by graphing the angles 180o and
180o. Then we draw a reference angle into the appropriate quadrants.
We now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QI:
x1 = 60o
Solution in QIII:
x2 =
180o + 60o =
120o
Since we are supposed to express the solutions in terms of radians we get
x1 =
/3
and x2 =
2
/3
Example 4:
Solve
for x in the interval
. Express the solutions in EXACT radians.
Step 1:
The solution interval for angle x is
. We will then isolate the trigonometric ratio by dividing both sides of the equal sign by
1.
We end up with
.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we find we find x = tan -1 (
)
Helpful Hint: It is often easier to work in degrees and then change the solutions back to radians. So let's change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x =
60o.
Step 3:
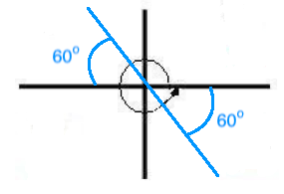
Given a solution for angle x in Step 2, we will find its reference angle. We know that the reference angle of a negative angle is equal to that of its positive counterpart.
Since 60o is a QI angle, its reference angle equals 60o. Therefore, the reference angle of
60o is 60o as well.
Step 4:
We have a reference angle and the value of the tangent ratio in Step 1 is negative.
Therefore, we will use All Students Take Calculus to find the quadrants in which the tangent ratio is positive. Thus, the tangent is negative in QII and QVI. See picture below!
Finally, let’s first indicate the solution interval for angle x by graphing the angle 360o. Then we draw the reference angle in the appropriate quadrants.
We now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QII:
x1 = 180o
60o = 120o
Solution in QIV:
x2 = 360o
60o = 300o
Since we are supposed to express the solutions in terms of radians we get
x1 = 2
/3
and x2 = 5
/3
Example 5:
Solve
for x in the interval
. Express the solutions in EXACT radians.
Step 1:
The solution interval for angle x is
. We will then isolate the trigonometric ratio by dividing both sides of the equal sign by 2.
We end up with
.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we find
.
Helpful Hint: It's easier to work in degrees and then change the solutions back to radians. So let's change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x = 45o.
Step 3:
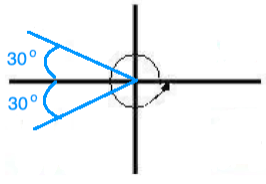
Given a solution for angle x in Step 2, we will find its reference angle. Since angle 45o is a QI angle, its reference angle equals 45o.
Step 4:
We have a reference angle and the value of the sine ratio in Step 1 is positive.
Therefore, we will use All Students Take Calculus to find the quadrants in which the sine ratio is positive. See picture below!
Finally, let’s first indicate the solution interval for angle x by graphing the angle 360o. Then we draw the reference angle in the appropriate quadrants.
We now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QI:
x1 = 45o
Solution in QII:
x2 = 180o
45o = 135o
Since we are supposed to express the solutions in terms of radians we get
x1 =
/4
and x2 = 3
/4
Example 6:
Solve
for x in the interval
. Express the solutions in EXACT radians.
Step 1:
The solution interval for angle x is
. We will then isolate the trigonometric ratio by dividing both sides of the equal sign by 2.
We end up with
.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we find
.
Helpful Hint: It's easier to work in degrees and then change the solutions back to radians. So, let’s change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x =
45o.
Step 3:
Given a solution for angle x in Step 2, we will find its reference angle. We know that the reference angle of a negative angle is equal to that of its positive counterpart. Since 45o is a QI angle, its reference angle equals 45o. Therefore, the reference angle of
45o is 45o as well.
Step 4:
We have a reference angle and the value of the sine ratio in Step 1 is negative.
Therefore, we will use All Students Take Calculus to find the quadrants in which the sine ratio is positive. Thus, the sine is negative in QIII and QVI. See picture below!
Finally, let’s first indicate the solution interval for angle x by graphing the angle 360o. Then we draw the reference angle in the appropriate quadrants.
We now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QIII:
x1 = 180o + 45o = 225o
Solution in QIV:
x2 = 360o
45o = 315o
Since we are supposed to express the solutions in terms of radians we get
x1 = 5
/4
and x2 = 7
/4
Example 7:
Solve cos x =
0.858 for x in the interval
in radians. Round all calculations to 3 decimal places.
Step 1:
The solution interval for angle x is
. The trigonometric ratio is already isolated on one side of the equal sign.
We use cos x =
0.858 .
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Note: Here it is not a good idea to work in degrees. The final solutions would become more and more inexact since we need to round to find the angle and then do more rounding to change from degrees to radians.
Given cos x =
0.858, we find x = cos-1 (
0.858).
With the calculator in radian mode, we get x
2.602.
Step 3:
Given a solution for angle x in Step 2, we will find its reference angle. Since 2.602 (
149o) is a QII angle, its reference angle is

2.602
0.540.
Step 4:
We have a reference angle and the value of the cosine ratio in Step 1 is negative.
Therefore, we will use All Students Take Calculus to find the quadrants in which the cosine ratio is positive. Thus, the cosine is negative in QII and QIII. See picture below!
Finally, let’s first indicate the solution interval for angle x by graphing the angle
. Then we draw the reference angle in the appropriate quadrants.
We can now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QII:
x1
2.602
Solution in QIII:
x2
+ 0.540
3.646
Example 8:
Solve sin x + 1 = 0 for x in the interval
. Express the solutions in degrees.
Step 1:
The interval in which we are supposed to find the solutions is
We end up with sin x =. We will isolate the trigonometric ratio by adding 1 to both sides of the equal sign.
1.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we get x = sin - 1(
1)
With the calculator in degee mode, we find x =
90o.
Step 3:
is a quadrantal angle, which has no reference angle!
Step 4:
Since we do not have a reference angle, we are going to show the following picture:
From the picture above, we find that sin x =
1 only at 270o on interval
.
Therefore, we have one solution, namely x = 270o.
Please note that the angle found in Step 2 is a perfectly good solution to the given equation. However, it does not lie in the solution interval [0o, 360o). Therefore, it is not a solution in our case.
Example 9:
Solve sin x
1 = 0 for x in the interval
. Express the solutions in degrees.
Step 1:
The interval in which we are supposed to find the solutions is
We end up with sin x = 1.. We will isolate the trigonometric ratio by adding 1 to both sides of the equal sign.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we get we get x = sin -1(1)
Therefore, with the calculator in radian mode, we find x = 90o.
Step 3:
is a quadrantal angle, which has no reference angle!
Step 4:
Since we do not have a reference angle, we are going to show the following picture:
From the picture above, we find that sin x = 1 only at 90o on interval
.
Therefore, we have one solution, namely
.
However, we must find the solutions in the interval
. We will simple add another 360o rotation to 90o to find a second solution, namely,
.
Example 10:
Find the general solution for
. Express it in EXACT radians.
Step 1:
We will find the solutions in the interval
first. We will isolate the trigonometric ratio by dividing both sidesof the equal sign by
2.
We end up with
.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we get
.
Helpful Hint: It's easier to work in degrees and then change the solutions back to radians. So, let’s change the solution interval to degrees, namely
, and then we continue to work with degrees.
With the calculator in degree mode, we get x = 150o.
Step 3:
Given a solution for angle x in Step 2, we will find its reference angle. Since 150o is a QII angle, its reference angle is 180o
150o = 30o.
Step 4:
We have a reference angle and the value of the cosine ratio in Step 1 is negative.
Therefore, we will use All Students Take Calculus to find the quadrants in which the cosine ratio is positive. Thus, the cosine is negative in QII and QIII. See picture below!
Finally, let’s first indicate the solution interval for angle x by graphing the angle 360o. Then we draw the reference angle in the appropriate quadrants.
We now find the solutions for angle x in the interval
with the help of the picture above.
Solution in QII:
x1 = 180o
30o = 150o
Solution in QIII:
x2 = 180o + 30o = 210o
Since we are supposed to express the solutions in terms of radians we get
x1 = 5
/6
and x2 = 7
/6
We are asked to find the general solution expressed in radians. We see in Step 4 that the solutions are NOT exactly
(or 180o) apart.
Therefore, we add 2
k to both solutions, where k is any integer.
The general solution for angle x is as follows:
5
/6 + 2
k and 7
/6 + 2
k
Example 11:
Find the general solution for 2cos x = 0. Express it in degrees.
Step 1:
We will find the solutions in the interval
first. We will isolate the trigonometric ratio by dividing both sides of the equal sign by 2.
We end up with cos x = 0.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given
, we get x = cod -1(0).
Therefore, with the calculator in degree mode, we find x = 90o.
Step 3:
is a quadrantal angle, which has no reference angle!
Step 4:
Since we do not have a reference angle, we are going to show the following picture:
From the picture above, we find that cos x = 0 at 90o and 270oon interval
.
Therefore, we have two solutions, namely x1 = 90o and x2 = 270o.
We are asked to find the general solutions expressed in degrees. We note that these two solutions are exactly 180o apart.
Therefore, to show the general solutions, we only need to add 180ok to the smaller of the two solutions in the interval between 0o and 360o where k is defined as any integer.
The general solution for angle x is 90o + 180ok.
Example 12:
Find the general solutions for 3tan x = 0. Express it in degrees.
Step 1:
We will find the solutions in the interval
We end up with tan x = 0.first. We will isolate the trigonometric ratio by dividing both sides of the equal sign by 3.
Step 2:
We are going to use the concept of Inverse Trigonometric Functions to solve for the angle x using the calculator.
Given tan x = 0, we get x = tan-1 (0)
Therefore, with the calculator in degree mode, we find x = 0o.
Step 3:
0o is a quadrantal angle, which has no reference angle!
Step 4:
Since we do not have a reference angle, we are going to show the following picture:
From the picture above, we find that tan x = 0 at 0o and 180o on interval
. Please note that the solution of 360o is excluded from the solution interval because the solution interval excludes this angle since there is a parenthesis next to it 360o !!!
Therefore, we have two solutions, namely x1 = 0o and x2 = 180o.
We are asked to find the general solutions expressed in degrees. We note that these two solutions are exactly 180o apart.
Therefore, to show the general solution, we only need to add 180ok to the smaller of the two solutions in the interval between 0o and 360o where k is defined as any integer.
The general solution for angle x is 0o + 180ok.