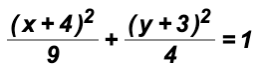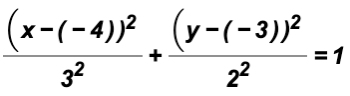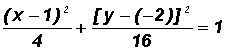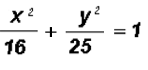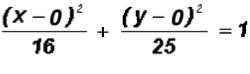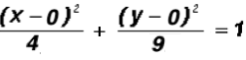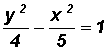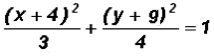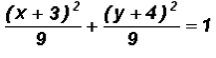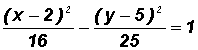CONIC SECTIONS - THE ELLIPSE

Example 1:

Write the standard equation of the following ellipse. Then find the coordinates of the center.

This equation is almost in standard form. All we have to do is the following:

where h = 4, k = 3, a = 3 (from larger denominator), and b = 2

The coordinates of the center are (4, 3).

Example 2:

Write the standard equation of the following ellipse. Then find the coordinates of the center.

First, we will convert the equation of the ellipse to standard form.

It is either or , where

First, we will divide both sides of the equation by 16 to get

 

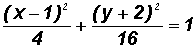
We can now write the standard form of the given elliptic equation as follows:

where h = 1, k = 2, a = 4 (from larger denominator), and b = 2

The coordinates of the center are (1, 2).

Example 3:

Write the standard equation of the following ellipse. Then find the coordinates of the center.

This equation is almost in standard form. It is either or , where

NOTE: The center (h, k) of the given ellipse is at (0, 0) because there is only an x²-term and a y²-term. Therefore, we can write

where h = 0, k = 0, a = 5 (from larger denominator), and b = 4

The coordinates of the center are (0, 0).

Example 4:

Write the standard equation of the following ellipse. Then find the coordinates of the center.

The standard form of this ellipse is either or , where .

First, we will divide both sides of the equation by 36 to get

We can now write the standard form of the given elliptic equation as follows:

where h = 0, k = 0, a = 3 (from larger denominator), and b = 2

The coordinates of the center are (0, 0).

Example 5:

Match the names hyperbola, ellipse, parabola, and circle to the following conic equations.

a.

We must recognize this as a hyperbola because of its general characteristics. There is a squared x and y-term and one of them is negative. It is actually a hyperbola with center at the origin.

b.

We must recognize this as an ellipse because of its general characteristics. There is a squared x and y-term and both are positive. Also, the squared terms have different denominators.

c.

We must recognize this as an ellipse because of its general characteristics. There is a squared x and y-term and both are positive. Also, the squared terms have different coefficients (or denominators).

d.

We must recognize this as a circle because of its general characteristics. There is a squared x and y-term and both are positive. Also, the squared terms have the same denominators.

e.

We must recognize this as a circle because of its general characteristics. There is a squared x and y-term and both are positive. Also, the squared terms have the same coefficients (or denominators), namely 1.

f.

We must recognize this as the standard form of a parabola because of its general characteristics. There is only one squared term, namely y².

g.

We must recognize this as a hyperbola because of its general characteristics. There is a squared x and y-term and one of them is negative.