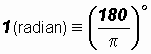TRIGONOMETRIC RATIOS OF MULTIPLES OF QUADRANTAL ANGLES

Example 1:

The angle 450^o is a quadrantal angle. Find the EXACT value of tan 450^o without a calculator.

Find a coterminal angle between 0^o and 360^o.

450 = 360^o(1) + 90^o

We find that 450^o is coterminal with 90^o.

 We will use the following memorized picture to find the value of tan 90^o.

We see that tan 90^o is undefined. Therefore, tan 450^o is also undefined.

Example 2:

The angle 9/2 is a quadrantal Angle. Find the EXACT value of sin (9/2) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees. If necessary use the following formula:

Find a coterminal angle between 0 and 2.

9/2 = 2(2) + /2 . We find that /2 90^o is coterminal with 9/2 810^o.

 We will use the following memorized picture to find the value of sin /2.

We see that sin /2 is equal to 1. Therefore, sin 9/2 is also equal to 1.

Example 3:

The angle 11/2 is a quadrantal angle. Find the EXACT value of sin (11/2) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

Find a coterminal angle between 0 and 2.

11/2 = 2(2) + 3/2. We find that 3/2 270^o is coterminal with 11/2990^o.

We will use the following memorized picture to find the value of sin 3/2.

We see that sin 3/2 is equal to 1.  Therefore, sin 11/2 is also equal to 1.

Example 4:

The angle 9 is a quadrantal angle. Find the EXACT value of cos (9) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

Find a coterminal angle between 0 and 2.

9 = 2(4) + . We find that 180^o is coterminal with 9 1620^o.

We will use the following memorized picture to find the value of cos (9).

We see that cos is equal to 1.  Therefore, cos (9) is also equal to 1.