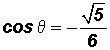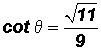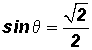TRIGONOMETRIC RATIOS OF ANGLES OF ANY MAGNITUDE - Part 1

Example 1:

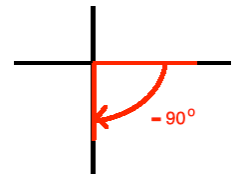
a. Graph the quadrantal angle 90o.

b. Find the smallest positive angle in degrees that is coterminal to 90o.

It is best to graph this situation.

We quickly see that the angle with measure 270o is the smallest positive angle that is coterminal with 90o.

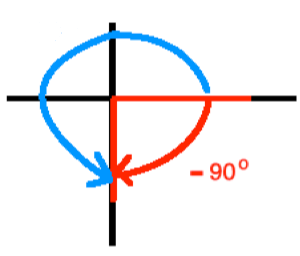
c. Find the smallest negative angle in degrees that is coterminal to 90o.

Please note that a negative sign simply indicates clockwise direction!

We quickly see that the angle with measure 90o + 360o = 450o is the smallest negative angle that is coterminal with 90o.

Example 2:

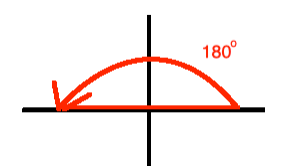
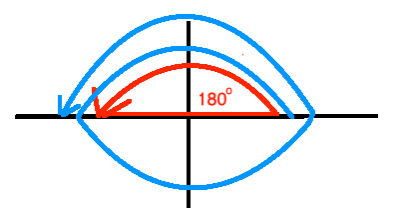
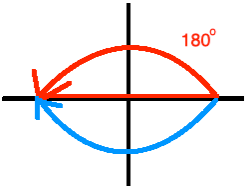
a. Graph the quadrantal angle 180o.

b. Find the smallest positive angle in degrees that is coterminal with 180o.

It is best to graph this situation.

We quickly see that the angle with measure 180o + 360o = 540o is the smallest positive angle that is coterminal with 180o.

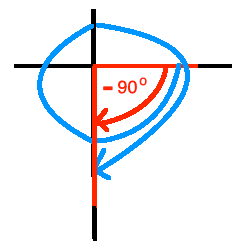
c. Find the smallest negative angle in degrees that is coterminal with 180o.

Please note that a negative sign simply indicates clockwise direction!

We quickly see that the angle with measure 180o is the smallest negative angle that is coterminal with 180o.

Example 3:

Find all angles that are coterminal with a 5pi.gif (853 bytes)/3 angle.

We can find angles that are coterminal to it by ADDING integer multiples of 2pi.gif (853 bytes). We will name the integer k to express ALL angles coterminal to 5pi.gif (853 bytes)/3 as follows:

5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)k, where k is any integer

For instance,

when k = 2, then 5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)(2) = 5pi.gif (853 bytes)/3 + 4pi.gif (853 bytes)

                                                  = 5pi.gif (853 bytes)/3 + 12pi.gif (853 bytes)/3 (need common denominator)

                                                  = 17pi.gif (853 bytes)/3

when k = 1, then 5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)(1) = 5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)

                                                  = 5pi.gif (853 bytes)/3 + 6pi.gif (853 bytes)/3 (need common denominator)

                                                  = 11pi.gif (853 bytes)/3

when k = 1, then 5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)(1) = 5pi.gif (853 bytes)/3 2pi.gif (853 bytes)

                                                        = 5pi.gif (853 bytes)/3 6pi.gif (853 bytes)/3 (need common denominator)

                                                        = pi.gif (853 bytes)/3

when k = 2, then 5pi.gif (853 bytes)/3 + 2pi.gif (853 bytes)(2) = 5pi.gif (853 bytes)/3 4pi.gif (853 bytes)

                                                        = 5pi.gif (853 bytes)/3 12pi.gif (853 bytes)/3 (need common denominator)

                                                        = 7pi.gif (853 bytes)/3

Example 4:

Find an angle between 0 and 2pi.gif (853 bytes) that is coterminal with the angle 11/2.

We can find an angle that is coterminal to 11/2 by SUBTRACTING from it integer multiples of 2pi.gif (853 bytes) until the difference is smaller than 2pi.gif (853 bytes). This difference is a coterminal angle.

11/2 = 8/2 + 3/2

           = 4 + 3/2

           = 2 + 2 + 3/2

We find that 3/2 is coterminal with 11/2.

Example 5:

Find an angle between 0o and 360o that is coterminal with the angle 1290o.

We can find an angle that is coterminal to 1290o by SUBTRACTING from it integer multiples of 360o until the difference is smaller than 360o. This difference is a coterminal angle.

1290o = 360o(3) + 210o.

We find that the angle 210o is between 0o and 360o and is coterminal with the 1290o angle.

Example 6:

Indicate in which two quadrants the terminal side of the following angles theta.gif (860 bytes) must lie.  Assume that theta.gif (860 bytes) is not a Quadrantal Angle.

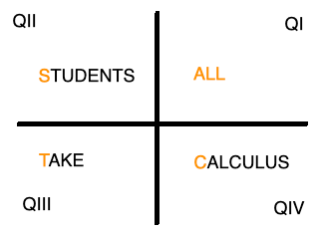
For this we will use "All Students Take Calculus" which indicates in which quadrant the numeric value of the trigonometric ratio of an angle is positive.

a.  

All Students Take Calculus - numeric value of cosine is positive in QI and QIV. Therefore, it is negative in QII and QIII.

b.  

All Students Take Calculus - numeric value of tangent is positive in QI and QIII.

c.  

All Students Take Calculus - numeric value of cotangent is positive in QI and QII. Therefore, it is negative in QII and QIV.

d.  

All Students Take Calculus - numeric value of sine is positive in QI and QII. Therefore, it is negative in QIII and QIV.

e.  

All Students Take Calculus - numeric value of cosine is positive in QI and QIV.

f.  

All Students Take Calculus - numeric value of tangent is positive in QI and QIII. Therefore, it is negative in QII and QIV.

g.  

All Students Take Calculus - numeric value of cotangent is positive in QI and QIII.

h. 

All Students Take Calculus - numeric value of sine is positive in QI and QII.

Example 7:

Indicate in which quadrant the terminal side of the following angles theta.gif (860 bytes) must lie.  Assume that theta.gif (860 bytes) is not a Quadrantal Angle.

For this we will use "All Students Take Calculus."

a. Identify the quadrant or quadrants for the angle theta.gif (860 bytes) satisfying the given condition.

and

All Students Take Calculus - numeric value of sine is positive in QI and QII, but only in QII is the numeric value of cosine negative. Therefore, in QII the given conditions are satisfied.

b. Identify the quadrant or quadrants for the angle theta.gif (860 bytes) satisfying the given condition.

and

All Students Take Calculus - numeric value of cosine is positive in QI and QIV, but only in QI is the numeric value of tangent is also positive. Therefore, in QI the given conditions are satisfied.

c. Identify the quadrant or quadrants for the angle theta.gif (860 bytes) satisfying the given condition.

and

All Students Take Calculus - numeric value of tangent and cotangent is positive in QI and QIII. Therefore, in QI and QIII the given conditions are satisfied.

d. Identify the quadrant or quadrants for the angle theta.gif (860 bytes) satisfying the given condition.

and

All Students Take Calculus - numeric value of tangent is positive in QI and QIII, but only in QIII is the numeric value of sine negative. Therefore, in QIII the given conditions are satisfied.

Example 8:

While we memorized that tan 90o is undefined, let's use the calculator to find it. 

The calculator must be in degree mode.

Input: tan 90o ENTER

We get a "domain error" message. Some calculators show the infinity symbol . This is the calculator's way if telling us that tan 90o is undefined.

Example 9:

While we memorized that the cot 90o equals 0, let's use the calculator to find it.

The calculator must be in degree mode!

It was mentioned in an earlier lecture, that the best identity to use to evaluate cotangent is the Quotient Identity .

Input: cos 90o sin 90o ENTER

The calculator gives us a value of 0.

NOTE:

Had we used the Reciprocal Identity .

Input: 1 tan 90o ENTER

The calculator gives us a "Domain Error" ?????? This is incorrect! What is happening?

Well, most calculators do not know how to handle 1undefined given that tan(90) is undefined. That's why it's always better to use the Quotient Identity for cotangent at all times.

Example 10:

While we memorized that csc 0o is undefined, let's use the calculator to find it. 

The calculator must be in degree mode.

We MUST use the Reciprocal Identity .

Input: 1sin 0o ENTER

We get an error message. (Some other calculators show the positive/negative infinity symbol .) This is the calculator's way if telling us that csc0o is undefined.

because we are dividing by 0

Example 11:

The angle 9/2 is a quadrantal Angle. Find the EXACT value of sin (9/2) without a calculator.

Please note that no calculator can be used on Exam 1!

Step 1

Find a coterminal angle between 0 and 2.

9/2 = 8/2 + /2

         = 4 + /2

         = 2 + 2 + /2

We find that /2 is coterminal with 9/2.

Step 2

We know that the values of trigonometric ratios of coterminal angles are identical.

Use the following fact which we memorized:

We find that both sin /2 and sin 9/2 must be equal to 1.

Example 12:

The angle 11/2 is a quadrantal angle. Find the EXACT value of sin (11/2) without a calculator.

Please note that no calculator can be used on Exam 1!

Step 1

Find a coterminal angle between 0 and 2.

11/2 = 8/2 + 3/2

           = 4 + 3/2

           = 2 + 2 + 3/2

We find that 3/2 is coterminal with 11/2.

Step 2

We know that the values of trigonometric ratios of coterminal angles are identical.

Use the following fact which we memorized:

We find that both sin 3/2 and sin 11/2 must be equal to 1.

Example 13:

The angle 9 is a quadrantal angle. Find the EXACT value of cos (9) without a calculator.

Please note that no calculator can be used on Exam 1!

Step 1:

Find a coterminal angle between 0 and 2.

9 = 8 +

      = 2 + 2 + 2 + 2 +

We find that is coterminal with 9.

Step 2:

We know that the values of trigonometric ratios of coterminal angles are identical.

Use the following fact which we memorized:

We find that both cos and cos 9must be equal to 1.

Example 14:

The angle cos 990o is a quadrantal angle. Find the EXACT value of cos 990o without a calculator.

Please note that no calculator can be used on Exam 1!

Step 1

Find a coterminal angle between 0o and 360o.

990o = 720o + 270o

        = 360o + 360o + 270o

We find that 270o is coterminal with 270o.

Step 2

We know that the values of trigonometric ratios of coterminal angles are identical.

Use the following fact which we memorized:

We find that both cos 270o and cos 990o must be equal to 0.