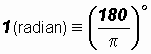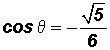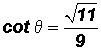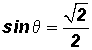TRIGONOMETRIC RATIOS OF MULTIPLES OF "SPECIAL" ANGLES

Example 1:

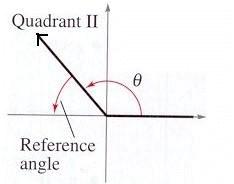
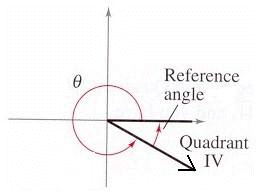
Find the reference angle of the following angles.

Let's use the pictures below as a guide.

                    

           

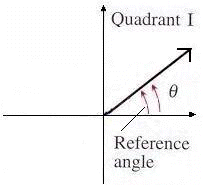
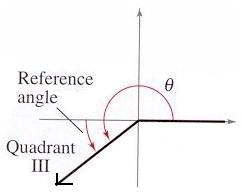
a. = 75^o

75^o it is a QI angle (hint: graph it). Its reference angle equals 75^o as well.

b. = 150^o

150^o it is a QII angle (hint: graph it). We calculate its reference angle as follows:

= 180^o 150^o = 30^o

c. = 225^o

225^o it is a QIII angle (hint: graph it). We calculate its reference angle as follows:

= 225^o 180^o = 45^o

d. = 300^o

300^o it is a QIV angle (hint: graph it). We calculate its reference angle as follows:

= 360^o 300^o = 60^o

e. = 135^o

This angle is not between 0^o and 360^o. Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, we learned that negative angles have the same reference angles as their positive counterparts, so let's use 135^o.

We will use 135^o which is a QII angle (hint: graph it). We calculate its reference angle as follows:

= 180^o 135^o = 45^o

It follows that the reference angle of 135^o is also 45^o.

f. = 315^o

This angle is not between 0^o and 360^o. Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, we learned that negative angles have the same reference angles as their positive counterparts, so let's use 315^o.

We will use 315^o which is a QII angle (hint: graph it). We calculate its reference angle as follows:

= 360^o 315^o = 45^o

It follows that the reference angle of 315^o is also 45^o.

g. = 11/6

NOTE: If radian measure is too uncomfortable for you, change it to degrees. If necessary use the following formula:

3/5 is a QIV angle (hint: 3/2 270^o)

We calculate its reference angle as follows:

= 211/6

    = 12/6 11/6

    = /6 30^o

The reference angle is /6 30^o. Note, here we had to use a common denominator before subtracting the fraction!

h. = 2/3

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

We need to find the reference angle. However, the given angle is not between 0 and 2.  Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, one of the four characteristics of reference angles states that negative angles have the same reference angles as their positive counterparts.  Therefore, we will find the reference angle using + 2/3 120^o.

2/3 is a QII angle (hint: 2/3 120^o).

We calculate its reference angle as follows:

= 2/3

    = 3/3 2/3

    = /3 60^o

The reference angle for 2/3 is /3 60^o which is also the reference angle for 2/3.

i. = 3/5

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

3/5 is a QII angle (hint: 3/5 108^o).

We calculate its reference angle as follows:

= 3/5

    = 5/5 3/5

    = 2/5 72^o

Note, here we had to use a common denominator before subtracting the fraction!

Example 2:

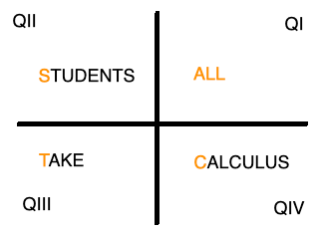
Use "All Students Take Calculus" to indicate in which quadrants the terminal side of the following angles must lie. 

a.  

All Students Take Calculus - numeric value of cosine is positive in QI and QIV. Therefore, it is negative in QII and QIII.

b.  

All Students Take Calculus - numeric value of tangent is positive in QI and QIII.

c.  

All Students Take Calculus - numeric value of cotangent is positive in QI and QII. Therefore, it is negative in QII and QIV.

d.  

All Students Take Calculus - numeric value of sine is positive in QI and QII. Therefore, it is negative in QIII and QIV.

e.  

All Students Take Calculus - numeric value of cosine is positive in QI and QIV.

f.  

All Students Take Calculus - numeric value of tangent is positive in QI and QIII. Therefore, it is negative in QII and QIV.

g.  

All Students Take Calculus - numeric value of cotangent is positive in QI and QIII.

h. 

All Students Take Calculus - numeric value of sine is positive in QI and QII.

Example 3:

Use "All Students Take Calculus" to indicate in which quadrants the terminal side of the following angles must lie.  Assume that is not a Quadrantal Angle.

a. Identify the quadrant or quadrants for the angle satisfying the given condition.

sin() > 0 and cos() < 0

All Students Take Calculus - numeric value of sine is positive in QI and QII, but only in QII is the numeric value of cosine negative. Therefore, in QII the given conditions are satisfied.

b. Identify the quadrant or quadrants for the angle satisfying the given condition.

cos() > 0 and tan() > 0

All Students Take Calculus - numeric value of cosine is positive in QI and QIV, but only in QI is the numeric value of tangent is also positive. Therefore, in QI the given conditions are satisfied.

c. Identify the quadrant or quadrants for the angle satisfying the given condition.

tan() > 0 and cot() > 0

All Students Take Calculus - numeric value of tangent and cotangent is positive in QI and QIII. Therefore, in QI and QIII the given conditions are satisfied.

d. Identify the quadrant or quadrants for the angle satisfying the given condition.

tan() > 0 and sin() < 0

All Students Take Calculus - numeric value of tangent is positive in QI and QIII, but only in QIII is the numeric value of sine negative. Therefore, in QIII the given conditions are satisfied.

Example 4:

The angle 150^o is a multiple of a special angle. Find the EXACT value of cos 150^o without a calculator.

Step 1 - Find the reference angle.

150^o is a QII angle (hint: graph it), therefore, it has the following reference angle:

= 180^o 150^o = 30^o

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

cos 30^o = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Use found in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of cos 150 is either or .


• According to "All Students Take Calculus", the cosine ratio has positive values in QI and QVI.  The terminal side of 150^o lies in QII (hint: graph it).  Consequently, cos 150^o must have a negative value. 

Specifically, cos 150^o must be equal to EXACTLY.

Example 5:

The angle 135^o is a multiple of a special angle. Find the EXACT value of sin (135^o) without a calculator.

Step 1 - Find the reference angle.

We need to find the reference angle. However, the given angle is not between 0^o and 360^o.  Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, one of the four characteristics of reference angles states that negative angles have the same reference angles as their positive counterparts.  Therefore, we will find the reference angle using +135^o.

135^o is a QII angle (hint: graph it), therefore, it has the following reference angle:

= 180^o 135^o = 45^o

(Then, 135^o also has a reference angle of 45^o.)

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

sin 45^o = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Use found in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of sin (135^o) is either or .


• According to "All Students Take Calculus", the sine ratio has positive values in QI and QII.  The terminal side of 135^o lies in QIII (hint: graph it).  Consequently, sin 135^o must have a negative value. 

Specifically, sin (135^o) must be equal to EXACTLY.

Example 6:

The angle 300^o is a multiple of a special angle. Find the EXACT value of cos 300^o without a calculator.

Step 1 - Find the reference angle.

300^o is a QIV angle (hint: graph it), therefore, it has the following reference angle:

= 360^o 300^o = 60^o

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

cos 60^o = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Use found in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of cos 300 is either or .


• According to "All Students Take Calculus", the cosine ratio has positive values in QI and QIV.  The terminal side of 300^o lies in QIV (hint: graph it).  Consequently,cos 300^o must have a positive value. 

Specifically, cos 300^o must be equal to EXACTLY.

Example 7:

The angle 315^o is a multiple of a special angle. Find the EXACT value of cos (315^o) without a calculator.

Step 1 - Find the reference angle.

We need to find the reference angle. However, the given angle is not between 0^o and 360^o.  Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, one of the four characteristics of reference angles states that negative angles have the same reference angles as their positive counterparts.  Therefore, we will find the reference angle using +315^o.

315^o is a QIV angle (hint: graph it), therefore, it has the following reference angle:

= 360^o 315^o = 45^o

(Then, 315^o also has a reference angle of 45^o.)

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

sin 45^o = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Use found in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of cos (315^o) is either or .


• According to "All Students Take Calculus", the sine ratio has positive values in QI and QII.  The terminal side of 315^o lies in QI (hint: graph it).  Consequently, cos (315^o ) must have a positive value. 

Specifically, cos (315^o) must be equal to EXACTLY.

Example 8:

The angle 495^o is a multiple of a special angle. Find the EXACT value of tan 495^o without a calculator.

Please note that no calculator can be used on Exam 1!

Step 1 - Find the reference angle.

We need to find the reference angle. However, this angle is not between 0^oand 360^o. Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, one of the four characteristics of reference angles states that coterminal angles have the same reference angle. We know that 495^o = 360^o(1) + 135^o, where 135^o is coterminal with 495^o.

Therefore, we will use 135^o to find the reference angle.

135^o is a QII angle (hint: graph it), therefore, it has the following reference angle:

= 180^o 135^o = 45^o

(Then, 495^o also has a reference angle of 45^o.)

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

tan 45^o = 1 We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Use 1 found in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of tan 495^o is either 1 or 1.


• According to "All Students Take Calculus", the tangent ratio has positive values in QI and QIII.  The terminal side of 495^o lies in QII (hint: graph it).  Consequently, tan 495^o must have a negative value. 

Specifically, tan 495^o must be equal to 1.

Example 9:

The angle 5/3 is a multiple of a special angle. Find the EXACT value of sin (5/3) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees. If necessary use the following formula:

Step 1 - Find the reference angle.

5/3 is a QIV angle (hint: 5/3 300^o), therefore, it has the following reference angle:

= 2 5/3       Note: You must know how to work with fractions!

     = 6/3 5/3

     = /3 60^o

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

sin (/3) = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Usefound in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of sin 5/3 is eitheror .


• According to "All Students Take Calculus", the sine ratio has positive values in QI and QII.  The terminal side of 5/3 300^o lies in QIV (hint: graph it).  Consequently, sin 5/3 must have a negative value. 

Specifically, sin (5/3) must be equal to EXACTLY.

Example 10:

The angle 5/6 is a multiple of a special angle. Find the EXACT value of tan (5/6) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

Step 1 - Find the reference angle.

5/6 is a QII angle (hint: 5/6 150^o), therefore, it has the following reference angle:

= 5/6      Note: You must know how to work with fractions!

     = 6/6 5/6

     = /6 30^o

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

tan (/6) = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Usefound in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of tan (5/6) is eitheror.


• According to "All Students Take Calculus", the tangent ratio has positive values in QI and QIII.  The terminal side of 5/6 150^o lies in QII (hint: graph it).  Consequently, tan 5/6 must have a negative value. 

Specifically, tan (5/6) must be equal to EXACTLY.

Example 11:

The angle 5/4 is a multiple of a special angle. Find the EXACT value of sin (5/4) without a calculator.

NOTE: If radian measure is too uncomfortable for you, change it to degrees.

Step 1 - Find the reference angle.

We need to find the reference angle. However, the given angle is not between 0^o and 360^o.  Therefore, we cannot use one of the four reference angle calculations we learned earlier.

However, one of the four characteristics of reference angles states that negative angles have the same reference angles as their positive counterparts.  Therefore, we will find the reference angle using + 5/4.

5/4 is a QIII angle (hint: 5/4 225^o ), therefore, it has the following reference angle:

= 5/4      Note: You must know how to work with fractions!

     = 5/4 4/4

     = /4 45^o

(Then, 5/4 also has a reference angle of /4.)

Step 2 - Find the value of the given trigonometric ratio of the reference angle.

sin (/4) = We memorized this!

Step 3 - Find the value of the trigonometric ratio of the given angle.

• Usefound in Step 2.


• We learned that the trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value. Therefore, the value of tan (5/6) is either or .


• According to "All Students Take Calculus", the sine ratio has positive values in QI and QII.  The terminal side of 5/4 225^o lies in QII (hint: graph it).  Consequently, sin (5/4 must have a positive value. 

Specifically, sin (5/4) must be equal to EXACTLY.