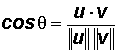INTRODUCTION TO VECTORS - PART 2
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.  Find the dot product of two vectors.
2.  Find unit vectors.
3.  Express vectors in terms of the i and j unit vectors.
4.  Find the angle between two vectors.
5.  Determine if two vectors are parallel, perpendicular, or equivalent.

Let's continue our introduction to vectors!

Dot Product - see #1 in the "Examples" document

Given two vectors u = and v = , their Dot Product is defined to be

=

is pronounced u dot v ! The Dot Product is a scalar and not a vector!

NOTE: YOU MUST MEMORIZE THIS FORMULA!

Unit Vector - see #2 and 3 in the "Examples" document

A vector with magnitude 1 is called a unit vector. Following are some frequently used unit vectors.

1.   Standard unit vectors with their special names i and j:

i =  and and j =

NOTE: YOU MUST MEMORIZE THESE VECTORS!

In handwritten documents you will often see and . There is a little "hat" over the i and j instead of a half arrow. A lot of times you will hear this pronounced as "i hat" and "j hat."

2.   Unit vectors with the same direction as a given nonzero vector v = .

We find these vectors by multiplying a vector v by a scalar comprised of the magnitude of v as follows;

NOTE: YOU MUST MEMORIZE THIS FORMULA!

Expressing a Vector in Terms of the Standard Unit Vectors - see #4 in the "Examples" document

In many applications it is necessary to express vectors in component form in terms of standard unit vectors. This is done as follows:

v = = i + j

The scalars and are called the horizontal and vertical components of vector v, respectively.

Angle Between Two Vectors - see #5 in the "Examples" document

The Law of Cosines is used to develop a formula to find the angle between two vectors. The angle is always between 0^o and 180^o.

Given a vector u and a vector v, the angle is found via the cosine ratio and its inverse.

That is,

The numerator in this fraction is a Dot Product, but the denominator is a simple multiplication of two real numbers!

Orthogonal, Parallel, and Equivalent Vectors - see #6 in the "Examples" document

Two vectors are orthogonal (90^o between them) if their Dot Product equals 0.

Two nonzero vectors u and v are parallel if there is some scalar c, such that u = cv.

Two vectors that have the same magnitude and direction are equivalent.