INTRODUCTION TO VECTORS - PART 1
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Use Vector Notation.
2.   Write a vector in component form.
3.   Find the magnitude of a vector.
4.   Find the direction of a vector.
5.   Add vectors.
6.  Multiply a vector with a scalar.
7.  Find the negative of a vector.
8.  Subtract vectors.

Many quantities in physics, such as area, time, and temperature, can be represented by a single number. Other quantities, such as force and velocity, must be represented by two numbers. Specifically, they require both magnitude and direction. To represent such quantities, we use something called a VECTOR.

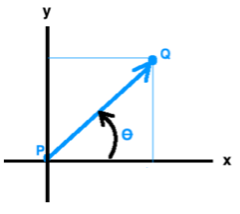
Let's draw a directed line segement (arrow on one end) making a positive angle with a horizontal line. Let's give it a beginning point P and an ending point Q at the tip of its arrow. The length of the directed line segment is the distance between P and Q.

Since we described the directed line segment in terms of an angle and a distance, we will now call it a VECTOR. Its direction is indicated by the positive angle . Its magnitude is the distance from point P to point Q. From now on we will call Point P the initial point and point Q the terminal point of a vector.

NOTE: When drawing a vector, there is always an arrow at the terminal point.

Vector Notation

Vectors are denoted by lowercase letters, usually u, v, or w, or by their initial and terminal point. 

In handwritten documents, a half arrow is placed over either notation.

For example, in the picture above we could call the vector or we could call it simply .

In printed documents, vector names are shown in bold print without the half arrow.

For example, PQ or v.

Standard Position of a Vector

A vector with its initial point at the origin of a Rectangular Coordinate System is said to be in standard position.

Definition of the Component Form of a Vector

Assume we have a vector in standard position and the coordinates of its terminal point Q are .

These coordinates are then used to write the vector in component form as , where q₁ and q₂ are called components.

NOTE: The component form of a vector requires angle brackets .

Example:

 

Write the following vector v in component form.

Using the coordinates of the terminal point, we find .

Finding the Component Form of a Vector - see #1 in the "Examples" document

If a vector is not in standard position, we can still find its component form. This also moves it to standard position.

Given a vector with initial point P at and terminal point Q at , its component form is found as follows:

NOTE: YOU MUST MEMORIZE THIS FORMULA!

For the first component, we subtract from the x-coordinate q₁ of the terminal point Q the x-coordinate p₁ of the initial point P. Similarly, for the second component, we subtract from the y-coordinate q₂ of the terminal point Q the y-coordinate p₂ of the initial point P.

Example:

Find the component form of a vector with initial point P at (1, 3) and terminal point Q at

(6, 5) . Name the vector v.

Given vector v = and points P and Q , we can calculate

v = < 6 (1), 5 (3) >, which equals v = < 5, 8 >.

Magnitude of a Vector - see #2 through 5 in the "Examples" document

The "length" of a vector is called magnitude. In physics it can represent speed, weight, etc.

The magnitude of a vector v = is denoted by ||v||.

It is found by using the Pythagorean Theorem on a vector in standard position and is

||v|| =

NOTE: YOU MUST MEMORIZE THIS FORMULA!

Example 3:

Calculate the EXACT magnitude of v = < 3, 2 >.

Given ||v|| = , we find||v|| =

Direction of a Vector - see #6 and 7 in the "Examples" document

Place the initial point of a vector at the origin in a coordinate system. Then the direction of the vector is given by the positive angle between the positive x-axis and the vector.We calculate using which we derived in the lesson on polar coordinates.

The x-value is the x-coordinate of the terminal point and the y-value is the y-coordinate of the terminal point.

Zero Vector

A zero vector can be denoted with a boldfaced 0 or. In component form it can be written as v = < 0, 0 >.

Vector Addition - see #8 in the "Examples" document