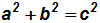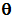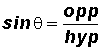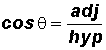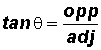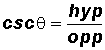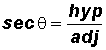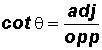THE SIX TRIGONOMETRIC RATIOS
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Define a right triangle and a unit circle.
2.   Memorize and use the six trigonometric ratios in a right triangle.
3.   Memorize and use the reciprocal and quotient identities.

We will now continue our study of trigonometry by defining six trigonometric ratios. They are fundamental to almost everything else we do in this course.

The six trigonometric ratios can be defined by using a right triangle or the unit circle. In this lecture, we will use the right triangle approach. Let's quickly review both.

Review - The Right Triangle

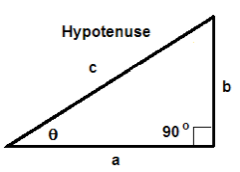
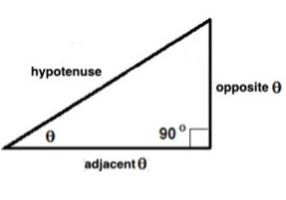
A triangle in which one angle is 90^o is called a right triangle. The side opposite the right angle is called the hypotenuse and the remaining two sides are called legs.

In the picture below, the length of the hypotenuse is c and the lengths of the two legs are a and b. 

The sides of a right triangle are related via the Pythagorean Theorem as follows: 

Review - The Unit Circle

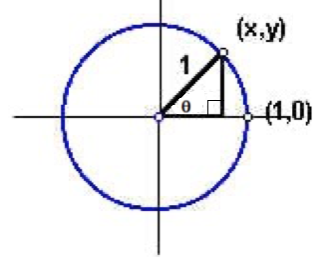
The unit circle is a circle of radius 1.

The equation of the unit circle in a rectangular coordinate system with center at the origin is .

Definition of the Six Trigonometric Ratios - see #1 through 4 in the "Examples" document

Trigonometric ratios are always based on some angle. We will use angle in a right triangle to define the six trigonometric ratios.

In the definitions of the trigonometric ratios, we will use the following abbreviation:

adj - the side of a right triangle adjacent to the angle

opp - the side of a right triangle opposite the angle

hyp - the hypotenuse of a right triagle

Sine Ratio: 

Pronounce sin as "sine theta".

Cosine Ratio: 

Pronounce cos as "cosine theta". 

Tangent Ratio: 

Pronounce tan as "tangent theta". 

Memorization Aid for the Sine, Cosine, and Tangent (there may be others):

SOHCAHTOA (Sine equals Opposite over Hypotenuse; Cosine equals Adjacent over Hypotenuse; and Tangent equals Opposite over Adjacent).

Cosecant Ratio:

Pronounce csc as "cosecant theta" (koseekent theta).

NOTE: The Cosecant Ratio is the reciprocal of the Sine Ratio!

Secant Ratio:

Pronounce sec as "secant theta" (seekent theta).

NOTE: The Secant Ratio is the reciprocal of the Cosine Ratio!

Cotangent Ratio:

Pronounce cot as "cotangent theta".

NOTE: The Cotangent Ratio is the reciprocal of the Tangent Ratio!

YOU MUST MEMORIZE THE SIX TRIGONOMETRIC IDENTITIES AS STATED ABOVE!

The Reciprocal and Quotient Identities - see #1 through 4 in the "Examples" document

In trigonometry, a great deal of time is spent studying relationships between trigonometric ratios. We call these relationships "identities." 

Reciprocal Identities - Let's use these identities to define the cosecant, secant, and cotangent ratios.

                    

                    

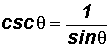
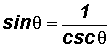
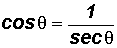
Quotient Identities - Let's use these identities to define the tangent and cotangent ratios in terms of the sine and cosine ratios.

          

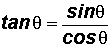
YOU MUST MEMORIZE THE RECIPROCAL AND QUOTIENT IDENTITIES!