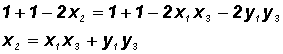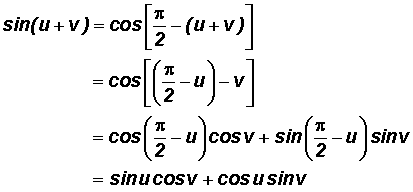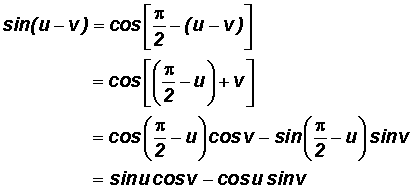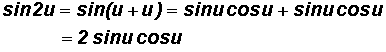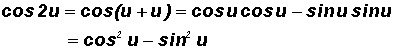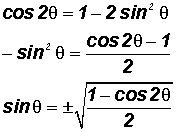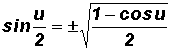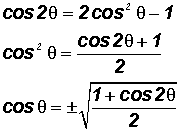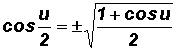POINT OF INTEREST 6
DIFFERENCE , DOUBLE, AND HALF ANGLE IDENTITIES
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Proof of the Difference Identity for Cosine

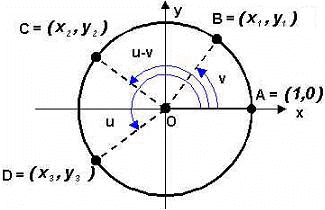
We will use the following picture for this proof:

Since the angles between the segment OA and OC and the segment OB and OD both measure (u v), the arcs AC and BD must have the same length. This implies that the line segments connecting points A and C and points B and D are also equal in length.  That is,

Raising both sides to the second power and combining like terms, we get

Notice that the parentheses contain circles. The value of the three quantities within the parentheses is 1 since , , and are points on a unit circle.

Therefore,

Finally, letting

                      

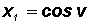
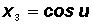
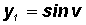
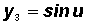
we get , which is usually presented as

Proof of the Sum and Difference Identities for Sine and

Given the Difference Identity for Cosine, it is easy to show that . We will use this fact to show a proof of the Sum and Difference Identities for Sine.

If we let , then we can prove a Sum Identity for Sine!

If we let , then we can prove a Difference Identity.

Incidentally, the Sum Identity for Cosine can be established using .

Proof of the Double Angle Identities for

Sine

To proof the first identity, let in the Sum Identity

Cosine

To proof the second identity, let in the Sum Identity

Proof of the Half Angle Identities for

Sine

Here we use the Double Angle Identity

Finally, let , then

Cosine

Here we use the Double Angle Identity

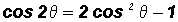
Finally, let , then