SUM AND DIFFERENCE IDENTITIES
DOUBLE ANGLE AND HALF ANGLE IDENTITIES
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
![]()
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Given the formulas for the Sum Identity, be able to work with them.
2. Given the formulas for the Difference Identity, be able to work with them.
3. Given the formulas for the Double Angle Identity, be able to work with them.
4. Given the formulas for the Half Angle Identity, be able to work with them.
So far we were exposed several useful trigonometric identities. Namely, the Reciprocal, Quotient, and Pythagorean Identities. We will now discuss a few other identities that can also be useful at times.
They DO NOT have to be memorized! However, you must know how to work with them when given to you.
Proofs are provided separately for some of the formulas for your information only. If you are interested you might want to look at them. They can be found under the link "Point of Interest 6" in the Learning Materials #14 in the MyOpenMath course.
Sum Identities - see #1 through 3 in the "Examples" document
Let u and v be any algebraic expression.
Difference Identities - see #1 through 3 in the "Examples" document
Let u and v be any algebraic expression.
Double Angle Identity for Sine - see #4 and 9 in the "Examples" document
Let u be any algebraic expression.
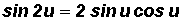
Double Angle Identity for Cosine - see #5 and 6 in the "Examples" document
Let u be any algebraic expression.
Primary Identity:
Secondary Identities (derived from manipulating the primary identity):
1. Replace
in the primary identity with
(from Pythagorean Identity)
then
2. Replace
thenin the primary identity with
(from Pythagorean Identity)
Double Angle Identity for Tangent:
There are other ways to show the Double Angle Identity for tangent, however, this is the easiest one and also the one we will use!
Let u be any algebraic expression.
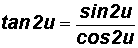
Half-Angle Identity for Sine - see #7 and 9 in the "Examples" document
Let u be any algebraic expression.
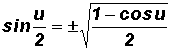
NOTE: The plus or minus sign in the half angle identities depends on the quadrant in which the angle
lies.
Half-Angle Identity for Cosine - see #8 in the "Examples" document
Let u be any algebraic expression.
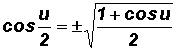
NOTE: The plus or minus sign in the half angle identities depends on the quadrant in which the angle
lies.
Half-Angle Identity for Tangent:
There are other ways to show the Half Angle Identity for tangent, however, this is the easiest one and also the one we will use!
Let u be any algebraic expression.