RIGHT TRIANGLE TRIGONOMETRY
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Find the angle of depression.
2.   Find the angle of elevation.
3.   Find the bearing.
4.   Solve right triangles.

Now that we know how to find angles when given trigonometric ratios, we will use trigonometry to model and solve a few application problems.

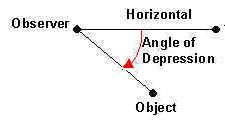
Angle of Depression - see #1 in the "Examples" document

When we look at something below our location, the angle between the line of sight and the horizontal is called the Angle of Depression. In this case, the line of sight is depressed below the horizontal.

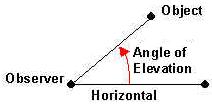
Angle of Elevation - see #2 in the "Examples" document

When we look at something above our location, the angle between the line of sight and the horizontal is called the Angle of Elevation. In this case, the line of sight is elevated above the horizontal.

Bearing - see #3 in the "Examples" document

In surveying and navigation, a direction is generally given in terms of a bearing which is an acute angle given together with compass headings (east, west, north, south).

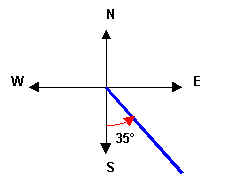
For example, S 35^o E (pronounced South 35^o East) or N 70^o W (pronounced North 70^o West).

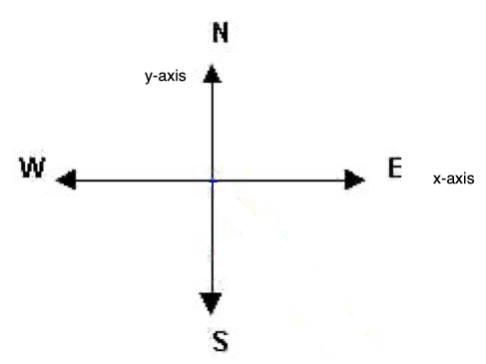
It is understood that the angle in a bearing is measured from a fixed north-south line toward an east-west line. The vertex of the angle is placed at the intersection of the two lines.

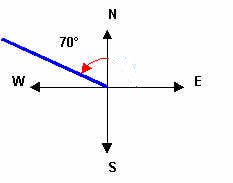
We can think of the north-south line as the y-axis in a retangular coordinate system and the east-west line as the x-axis. See picture below.

Examples:

Given is a bearing of S 35^o E. "South" tells you that the initial side of the angle is the "negative y-axis" and "East" tells you that the terminal side of the angle will be to the right of the "y-axis" (toward east).

Given is the bearing of N 70^o W". North" tells you that the initial side of the angle is the "positive y-axis" and "West" tells you that the terminal side of the angle will be to the left of the y-axis (toward west).

Solving Right Triangles - see #4 and 5 in the "Examples" document

The process of finding the missing measurements in a triangle knowing some measurements is known as "solving the triangle". We are going to solve right triangles by using the Pythagorean Theorem and the definitions of the trigonometric ratios.

We learned that the sides of a right triangle are related via the Pythagorean Theorem which states where c is the length of the hypotenuse and a and b are the length of the legs.

Previously, we defined the six trigonometric ratios for some angle in a right triangle as follows:

                           

                  

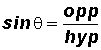
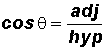
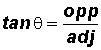
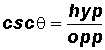
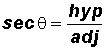
In the formulas, we used the following abbreviation:

adj - the side of a right triangle adjacent to the angle

opp - the side of a right triangle opposite the angle

hyp - the hypotenuse of a right triagle

Memorization Aid for the Sine, Cosine, and Tangent:

SOHCAHTOA (sine equals opposite over hypotenuse; cosine equals adjacent over hypotenuse; and tangent equals opposite over adjacent).