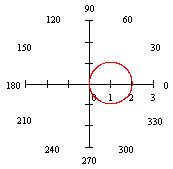GRAPHS OF SOME INTERESTING POLAR EQUATIONS
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Memorize the general polar forms of circles and associate them with their graphs.
2.   Find the radius of a circle equation in polar form.
3.   Associate the names of limaçons with their graphs.
4.   Recognize the graphs of Rose Curves given their polar form and find the number of petals.

Many polar equations have graphs we already studied in algebra (e.g., lines, parabolas). In this lesson we will discuss a few polar equations whose graphs we did not encounter in algebra. However, we will also revisit circles which we already studied in algebra, but this time their equations will be in polar form.

Limaçons

Pronounced lim-uh-sons which is French for "snail". The ç (pronounced c cedilla) is a special French letter. It is a "c" with a hook (cedilla) on the bottom.

where a and b are greater than 0

There are four different types of Limaçons. Their location in the polar coordinate system depends on whether sine or cosine are present.

You must memorize their pictures together with their names

Convex Limaçon when . It is almost a circle!

Dimpled Limaçon when.

Heart-Shaped Limaçon also called a Cardioid when . As compared to the Dimpled Limaçon, the "dimple" is more pronounced in the Cardioid.

Limaçon with inner loop when .

Rose Curves

Their equations are

, where a and n are NOT equal to 0 and n is NOT equal to 1

Following are examples of graphs of rose curves. Their location in the polar coordinate system depends on whether sine or cosine is present.

You must know the pictures of Rose Curves.

The number of petals depends on whether the angle multiplier n is odd or even.

When n is odd:

The rose curve has n petals. You must memorize this.

When n is even:

The rose curve as 2n petals.You must memorize this.

Circle Equations in Polar Form

You must memorize their equations.

r = a sin , a > 0 (See #1 in the "Examples" document for Polar Equations.)

The graphs of r = a sin have their center somewhere along a vertical r-axis. The radius is . You must know this.

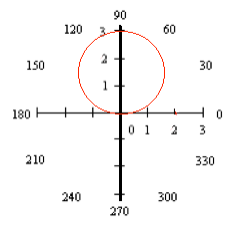
Example:

r = 3 sin equation of a circle with center at (0. 1.5) and radius 1.5.

r = a cos , a > 0 (See #5 in the "Examples" document for Polar Equations.)

The graphs of r = a cos have their center somewhere along the polar axis. The radius is .You must know this.

Example:

r = 2 cos equation of a Circle with center at (1,0) and radius 1.

r = a, a > 0 (See #3 and 6 in the "Examples" document for Polar Equations.)

The graphs of r = a have their center at the pole. The radius is a. You must know this.

PLEASE NOTE THAT THERE IS NO ANGLE IN THIS EQUATION. THIS IS UNLIKE THE OTHER CIRCLES, THE LIMAÇONS, AND THE ROSE CURVES. Actually, this means that there is no restriction on . It can take on any value as r stays a fixed number a.

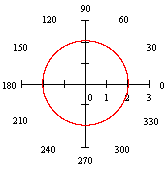
Example:

equation of a Circle with center at (0,0) and radius 2