POLAR EQUATIONS
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Change polar equations into rectangular equations.
2. Change rectangular equations into polar equations.
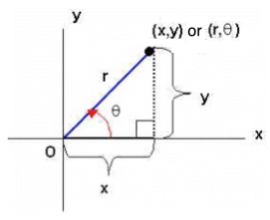
It is often also necessary to transform equations from rectangular to polar form or vice versa. The following polar-rectangular relationships are still useful in this regard.
standard form of the equation of a circle with center at the origin
(derived from the cosine ratio)
(derived from the sine ratio)
(derived from the tangent ratio)
Strategy for Changing Equations in Rectangular Form to Polar Form - see #1 through 4 in the "Examples" document
1. Use one or more of the the conversions
,
,
, and
2. Write this polar equation as r in terms of
. Writing r in therms of
Strategy for Changing Equations in Polar Form to Rectangular Form - see #5 through 9 in the "Examples" document
1. Use one or more of the conversions
2. If a conversion is not readily apparent, you must try one or more of the following:
- Multiply both sides of the equation by r
- Use the Reciprocal or Quotient Identities to change to sines and cosines
- Square both sides of the equation
