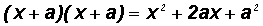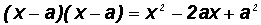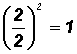A REVIEW OF SQUARE COMPLETION
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Square Completion is carried out to achieve perfect square trinomials of the following form:

or

Please not that

equals 

equals

IMPORTANT: Notice that the third term of either of the two trinomials above is found by dividing the coefficient 2a of the second term (x-term) by 2 and raising the result to the second power

The Square Completion Strategy Given a Quadratic Equation in Two Variables

1. Isolate or on one side of the equation.
2. If necessary, change the coefficient of to 1.
3. Find by dividing the coefficient of the x-term, which is 2a, by 2 and raising the result to the second power.
4. You then add to both sides of the equation!  This ensures that equality is preserved.  See WARNING below!

WARNING:  Should you have changed the coefficient of by factoring out a number, say k, you must add/subtract !

Example 1:

Given the equation complete the square on the right side

Step 1:

Isolate the terms containing x on one side of the equation.

y = x² x

Step 2:

Let's multiply both sides of the equation by 2 to change the coefficient of to 1.

2y + 1 = x² + 2x

Step 3:

Find by dividing the coefficient of the x-term, which is 2, by 2 and raising the result to the second power.

That is,

Step 4:

We then add 1 form Step 3 to both sides of the equation!  This ensures that equality is preserved.

2y + 1 + 1 = x² + 2x + 1

2y + 2 = x² + 2x + 1

and 2y + 2 = (x + 1)²

As requested in the instructions, we completed the square on the right side of the equation. 

Example 2:

Given the equation x = 2y² 12y + 7 complete the square on the right side.

Please note that we will use the above strategy, however, we will separate the y-terms from the x and the constant.

Step 1:

Isolate the terms containing y on one side of the equation.

x 7 = 2y² 12y

Step 2:

Let's factor 2 out of the right side to change the coefficient of to 1.

x 7 = 2(y² 6y)

Step 3:

Find by dividing the coefficient of the y-term, which is 6, by 2 and raising the result to the second power.

That is, .

Step 4:

So do we now add 9 from Step 3 to both sides of the equation? NO!

Please note that we CANNOT just add a 9 to the left side. This would change the value of the expression!  Actually we must add 2(9) because that's what we did on the right side too! Please study the following equation carefully!

x 7 + 2(9) = 2(y² 6y + 9)

Are you noticing that we actually added 2(9) to the right side?

and x + 11 = 2(y 3)²

As requested in the instructions, we completed the square on the right side of the equation.