INTRODUCTION TO CONIC SECTIONS - THE PARABOLA
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
![]()
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Memorize the characteristics of the focus, the directrix, and the latus rectum.
2. Memorize which standard form pertains to what graphs.
3. Change any equation to standard conic form.
2. Find the coordinates of the focus and the vertex.
3. Find the equation of the directrix.
![]()
In the next three lessons, we are getting away entirely from trigonometry, and very briefly investigate a few concepts in analythic geometry. Namely, we will introduce conic sections.
A conic section (or simply a conic) can be described as the intersection of a plane with two cones stacked tip to tip. The most common intersections are the parabola, the hyperbola, the circle, and the ellipse.
Let's discuss the parabola first!
The Conic Section resulting in a Parabola - see #1 through 4 in the "Examples" document
In algebra, we discussed quadratic functions and their graphs called parabolas. Their standard form
.
when a < 0 and
when a > 0
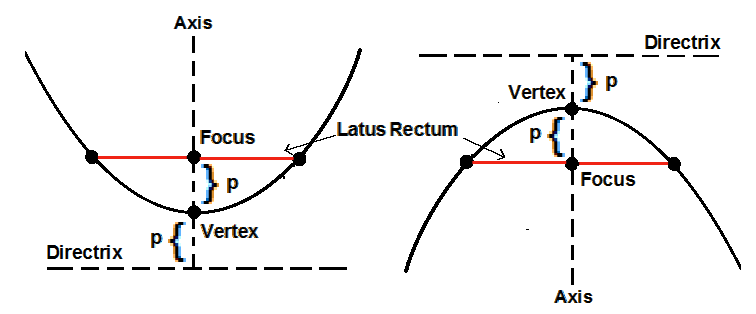
Parabolas can also be given a geometric definition. It is based on a point called focus and a fixed line called directrix.
Geometrically, a parabola is defined to be the set of all points that are always the same distance away from the directrix and the focus. Parabolas resulting form conic sectioning can be open up, down, right or left.
The focus is a distance, often called p, away from the vertex of the parabola and also lies along the axis of symmetry.
The directrix is perpendicular to the axis of symmetry and is also a distance p away from the vertex, but lies on the opposite side of the focus.
Parabolas Open Up or Open Down:
p > 0 p < 0
Note the line sement called latus rectum. It is is often helpful when graphing a parabola. It passes through the focus, is parallel to the directrix, and has its endpoints on the parabola.
Standard Form of the equation of a parabola is
. If p > 0 the parabolas are open up. If p < 0 the parabolas are open down.
You must know that this standard form pertains to parabolas open up and down.
You do not need to memorize the following information, however, you must know how to work with it when given.
Coordinates of the Focus are (h, k + p).
Coordinates of the Vertex are (h, k).
Equation of the Directrix is y = k
p.
Parabolas Open Right or Open Left:
p > 0 p < 0
Standard Form of the equation of a parabola is
. If p > 0 the parabolas are open right. If p < 0 the parabolas are open left. down.
You must know that this standard form pertains to parabolas open right and left.
You do not need to memorize the following information, however, you must know how to work with it when given.
Coordinates of the Focus are (h + p, k).
Coordinates of the Vertex are (h, k).
Equation of the Directrix is x = h
p.