INTRODUCTION TO PARAMETRIC EQUATIONS
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Find a set of parametric equation for some rectangular equations.
2. Find a rectangular equation for some sets of parametric equations.
In this final lesson, we will once again use some trigonometry, and this time to explain the concept of parametric equations.
Up to this point, we have been representing the graphs of functions and non-functions (e.g., circles, ellipses, vertical lines) by a single equation involving two variables, such as x and y or r and
. Now we will study a few situations in which we will describe these functions and non-functions in a different way.
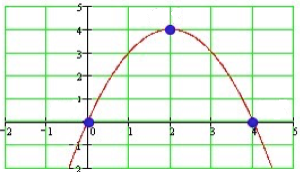
To start out, let's look at the function y =
x2 + 4x. From algebra we know that this is a quadratic function and its graph is a parabola open down. Following is its graph.
Let's assume that this parabola describes the path of an object catapulted into the air. What this graph does not tell us is the direction of movement of the object. Is it traveling from the left to the right along the curve or is it traveling from the right to the left?
To determine this, we will introduce a THIRD variable, called the parameter. Using this parameter, we will then create two separate equations, one for the x-variable and one for the y-variable in the functions or non-functions. We call this parameterizing a function or non-function.
As we know, there are infinitely many functions and non-functions in real life. Each and every one can be parameterized. However, in this introduction we will only discuss a few cases, namely functions and circles and ellipses which are not functions. Moreover, we will only examine circles and ellipses with center at the origin.
Please be aware that during the parameterization process, we always find TWO (2) equations. This is also called finding a SET of equations!
Parameterizing Functions in x and y - see #1 and 2 in the "Examples" document
Strategy:
(1) Decide on the name of the parameter. Most commonly in mathematics it involves the letter t.
We can just use t or any other expression, such as
(2) Replace the x-variable of the function with the parameter. This is our first parametric equation. It actually represents the x-coordinates of all the points on the graph of function.
(3) Express they-variable in terms of the parameter. This is our second parametric equation. It represents the y-coordinates of all the points on the graph of the function.
Parameterizing Circles and Ellipses in x and y with Center at the Origin - see #3 through 6 in the "Examples" document
When discussing conic sections, we were introduced to the standard form of circles and ellipses with center at the origin.
Specifically, the equation of a circle with center at the origin is expressed as
or
where a = b.
On the other hand, in standard form of the equation of an ellipse with center at the origin is expressed as
b.
Strategy:
(1) If necessary, change the equation to standard form
(2) Use the Pythagorean Identity sin2(t) + cos2(t) = 1 which is [sin(t)]2 + [cos(t)] = 1where t is the parameter
Let sin(t) either equal
or
.
NOTE: Our decision depends on the desired direction of movement of an object around a circle or ellipse. Is it going to be clockwise or counter-clockwise?
Express the equation in terms of x or y. This is our first parametric equation.
Thereafter, let cos(t) appropriately equal eitherExpress the equaiton in terms of x or y. This is our second parametric equation.
Finding an Equation in x and y for a Set of Parametric Equations NOT Containing Trigonometric Ratios - see #7 in the "Examples" document
Strategy:
(1) Isolate the parameter in either of the two parametric equations.
Note: "isolate" means that the parameter must be on one side of the eqquation by itself and must have a coefficient of 1.
(2) Substitute the resulting expression (in x or y) for the parameter in the "other" parametric equation. Then simplify if necessary or desired.
Finding an Equation in x and y for a Set of Parametric Equations Containing Trigonometric Ratios - see #8 and 9 in the "Examples" document
Strategy:
(1) Isolate the sine and cosine ratios on one side of their parametric equations.
Note: "isolate" means that the sine and cosine ratios must be on one side of the equation by themselves and must have a coefficient of 1.
(2) Replace cos(t) and sin(t) in the Pythagorean Identity sin2(t) + cos2(t) = 1 which is [sin(t)]2 + [cos(t)] = 1 with the "other sides" of their equations (see Step 1).
