TRIGONOMETRIC RATIOS OF ACUTE ANGLES
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
![]()
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Find values of trigonometric ratios of acute angles on the calculator in degrees and radians.
2. Memorize the EXACT values of trigonometric ratios of the "special" angles 30o, 45o, and 60o.

Finding Values of Trigonometric Ratios using a Calculator - see #1 through 9 in the "Examples" document
In the previous lecture, we found values of the six trigonometric ratios of an angle
using the sides of a right triangle. You may have noticed that we did not need actual angle measures to do this.
In this lecture, we will find the value of each trigonometric ratio when the angle measure is known. For example, sin 54o or cos 1.3 (radians).
We will most often use a calculator to find values of trigonometric ratios given angles. It utilizes a program using concepts from advanced calculus.
Let's look at two different Scientific Calculators, the TI-30X IIS and the TI-30XS. If you have a different calculator YOU must know how to use it.

Both calculators have a sin, cos, and tan button. They do NOT have a button for csc, sec, and cot !!! We MUST find the values of secant, cosecant, and cotangent on the calculator by using the Reciprocal and/or Quotient Identities.
NOTE: The
,
, and
buttons on the calculators do NOT find the values of cosecant, secant, and cotangent !!! These buttons calculate the inverse sine, inverse cosine, and inverse tangent which will be discussed later.
A calculator must be told to evaluate radians or degrees. Using the wrong mode will give you false information!!!
In the TI-30X IIS calculator you must locate the DRG button. It is in the first button row under the display window. Press it and observe the modes DEG, RAD, or GRD in the display window. Use the arrow buttons (located under the display window) to highlight the desired mode. Then press the Enter button to exit. In the lower right-hand corner of the display window you will then see what mode your calculator is in.
In the TI-30XS calculator you must locate the mode button. It is in the first button row under the display window. Press it and observe the modes DEG, RAD, or GRD in the display window. Use the arrow buttons (located under the display window) to highlight the desired mode. Then press the enter button. Finally, press the clear button to exit mode. In the upper right-hand corner of the display window you will then see what mode your calculator is in.
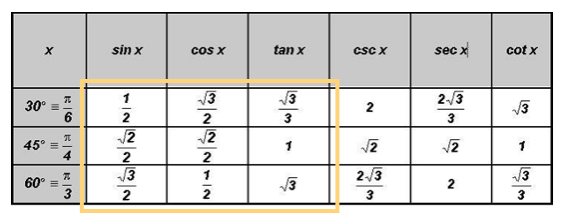
EXACT Values of Trigonometric Ratios of "Special" Angles - see #10 through 14 in the "Examples" document
Mathematicians, physicists, and engineers are obsessed with using EXACT values as much as possible. While most values of trigonometric ratios cannot be expressed as EXACT numbers, the values of trigonometric ratios of the "special" angles 30o, 45o, and 60o can. These EXACT numbers are used almost exclusively in application problems.
Since these values appear so often, it is common practice to force trigonometry students to memorize the values of trigonometric ratios of special angles instead of using the calculator to find them.
Please note that
is considered an EXACT number, while its decimal approximation 1.732 is not considered to be exact.
In the table below find the EXACT values of the trigonometric ratios of these "special" angles. If you are interested where these values came from, please read the documents found under the link "Point of Interest 1" in the Learning Materials #4 in the MyOpenMath course.
YOU MUST MEMORIZE THE VALUES OF ALL OF THE TRIGONOMETRIC RATIOS GIVEN THE SPECIAL ANGLES!
Memorization Hint: Only memorize the values for sine, cosine, and tangent. Then use the Reciprocal and/or Quotient Identities to find the remaining values.
Please observe the following decimal approximations for the EXACT values of trigonometric ratios of the "special" angles 30o, 45o, and 60o.
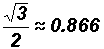
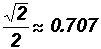
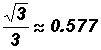
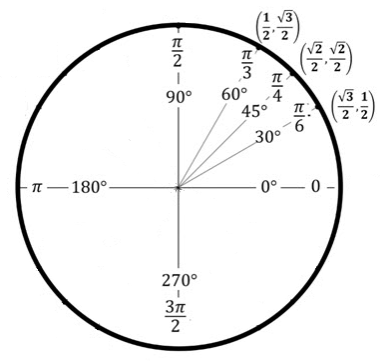
Some students who have had trigonometry in the past might have memorized the values of the trigonometric ratios of the "special" angles using the unit circle.
The x-coordinates of the points on the circle above are the values of cosine of certain special angles and the y-coordinates are the values of sine. The values of the tangent can be calculated using the Quotient Identity.