THE LAWS OF SINES AND COSINES
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Solve oblique triangles using the Law of Sines.
2.   Solve oblique triangles using the Law of Cosines.

In a previous lesson, we learned how to use the trigonometric ratios and the Pythagorean Theorem to find missing sides and angles in a right triangle. We called this process "solving a triangle." Now, we will learn how to do the same for oblique triangles, that is, triangles that do NOT contain a right angle. 

Some oblique triangles can be solved using the Law of Sines for others we must use the Law of Cosines. These laws can also be used with right triangles.

The Law of Sines - see #1 through 3 in the "Examples" document

To use the Law of Sines, we must be given at least one angle and its opposite side. You do not have to memorize the Law of Sines, however, you must know how to work with it when given.

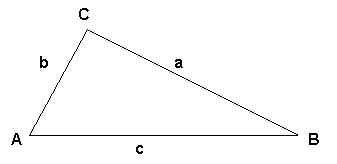
Given a triangle with angles A, B, and C, and opposite sides labeled a, b, and c, as shown in the picture below, then

or

The proof for this law is provided separately.  If you are interested, it can be found under the link "Point of Interest 4" in the Learning Materials #15 in the MyOpenMath course.

Please note that the Law of Sines sometimes produces two different sets of solutions!

The Law of Cosines - see #4 and 5 in the "Examples" document

When the Law of Sines cannot be applied, we must use the Law of Cosines. You do not have to memorize the Law of Cosines, however, you must know how to work with it when given.

NOTE: Once we start using this law, we continue to do so for all calculations even if we could switch to the Law of Sines eventually.

Given a triangle with angles A, B, and C, and opposite sides labeled a, b, and c, as shown in the picture below, then

Likewise, we can write the Law of Cosines for the other two sides as follows:

The proof for this law is provided separately.  If you are interested, it can be found under the link "Point of Interest 5" in the Learning Materials #15 in the MyOpenMath course.