INVERSE TRIGONOMETRIC FUNCTIONS
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Memorize the domain and range of the inverse sine function.
2. Memorize the domain and range of the inverse cosine function.
3. Memorize the domain and range of the inverse tangent function.
4. Use inverses to find angle measures.
In this lesson, we will study inverse trigonometric functions. As a reminder, we will start out with a review of inverse functions in algebra. Once we know about inverse trigonometric functions, we can find angles given a trigonometric ratio.
Review of Inverse Functions in Algebra!
From algebra you should remember that inverse functions are found by exchanging the dependent and independent variable. During this exchange, the domain and range are also switched.
However you can do this IF AND ONLY IF the function is ONE-TO-ONE. One-to-one function are special function where the range values never repeat.
We can determine that a function is NOT one-to-one if there is even one horizontal line that crosses its graph more than once!
For instance, f(x) =
(x
Imagine drawing the horizontal line y = 3 through the graph. As we can see, it goes through the points (0, 3) and (2, 3). The range value 3 repeats!
Now, if we restrict the domain of f(x) =
1, then we have a function that is one-to-one. Following is the graph.
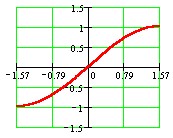
Finding the Inverse Sine Function
The sine function y = sin x is periodic and therefore NOT one-to-one. Just imagine drawing a horizontal line through its graph. This line will intersect with many points containing the same y-value.
In order to find its inverse, we must first restrict its domain which concists of all real numbers.
In trigonometry, we use the following domain restriction:
(input is angles in radians)
This gives us a range of
. See graph below.
The function is now one-to-one and we can find its inverse. We will excange x and y in y = sin x, to get x = sin y. This is the inverse sine function.
However, in trigonometry, we do not leave it in this form. It is rewritten as follows:
y = arcsin x
or
Both are pronounced either as arcsine of x or sine inverse of x!
During this exchange, the domain and range are also switched and we get the following for the inverse sine function:
Domain:
Range:
or
y
Please note, that the output consists of negative angles in QIV and positive angles in QI !!!
NOTE: YOU MUST MEMORIZE THE DOMAINS AND RANGES OF THE INVERSE TRIGONOMETRIC SINE FUNCTION. IT WILL BECOME IMPORTANT VERY SOON.
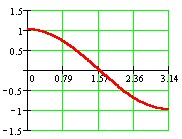
Finding the Inverse Cosine Function
The cosine function y = cos x is also periodic and therefore also NOT one-to-one. In order to find its inverse, we must first restrict its domain which consists of all real numbers.
In trigonometry, we use the following restriction:
(input is angles in radians)
This gives us a range of
The function is now one-to-one and we can find its inverse. We will excange x and y in y = cos x to get x = cos y. This is the inverse sine function.
However, in trigonometry, we do not leave it in this form. It is rewritten as follows:
y = arccos x
or
Both are pronounced either arccosine of x or cosine inverse of x!
During this exchange, the domain and range are also switched and we get the following for the inverse cosine function:
Domain:
Range:
or 0o
Please note, that the output (range) consists positive angles in QI and QII.
NOTE: YOU MUST MEMORIZE THE DOMAINS AND RANGES OF THE INVERSE TRIGONOMETRIC COSINE FUNCTION. IT WILL BECOME IMPORTANT VERY SOON.
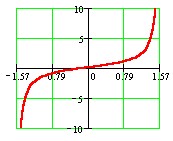
Finding the Inverse Tangent Function
The tangent function y = tan x is periodic as well and therefore also NOT one-to-one. In order to find its inverse, we must first restrict its domain which consists of all real numbers except all number of the form
.
In trigonometry, we use the following restriction:
(input is angles in radians)
Please note that the end values are NOT included because there the tangent function is undefined.
This gives us a range consisting of "all real numbers". See graph below.
The function is now one-to-one and we can find its inverse. We will excange x and y in y = tan x to get x = tan y. This is the inverse sine function.
However, in trigonometry, we do not leave it in this fom. It is rewritten as follows:
y = arctan x
or
Both are pronounced either arctangent of x or tangent inverse of x!
During this exchange, the domain and range are also switched and we get the following for the inverse tangent function:
Domain: all real numbers
Range:
or
Please note, that the output (range) consists of negative angles in QIV and positive angles in QI !!!
NOTE: YOU MUST MEMORIZE THE DOMAINS AND RANGES OF THE INVERSE TRIGONOMETRIC TANGENT FUNCTION. IT WILL BECOME IMPORTANT VERY SOON.
The Inverse Cotangent, Secant, and Cosecant Functions
For completeness sake, the definitions of the inverse cotangent, secant, and cosecant functions are included. However, we are not going to work with them in this course.
or
Domain:
Range:
(output is angles in radians)
or
Domain:
Range:
,
(output is angles in radians)
or
Domain:
Range:
,
(output is angles in radians)
Please note that the ranges (outputs) of the inverse secant and cosecant functions are not universally agreed upon!
Using Inverses to Find Angle Measures - see #1 through 9 in the "Examples" document
Now that we know about inverse trigonometric functions, we can find angles given a trigonometric ratio. For this we must often use a calculator. Let's look at the TI-30X IIS scientific calculator.
NOTE: It is very important to remember that a calculator will give us angles lying in the range of each inverse function.
Be sure the calculator is in the correct mode! If you want an angle in degrees, the calculator must be in degree mode. However, if you want an angle in radians, the calcuator must be in radian mode.
The inverse trig functions are above the sin, cos, and tan buttons! See picture!
We activate the sin-1, cos-1, or tan-1 function by pressing the 2nd button followed by the “sin”, “cos”, or “tan” button.
Left parenthesis will open when you activate sine, cosine, or tangent. Specifically, you will see sin-1 ( , cos-1 ( , or tan-1 ( .
After you type the numeric value, you MUST type the right parenthesis, namely ), before you press ENTER.
