INTRODUCTION TO POLAR COORDINATES
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Memorize the definition of the polar coordinate system.
2.   Graph points in the polar coordinate system.
3.   Change polar coordinates into rectangular coordinates.
4.   Change rectangular coordinates into polar coordinates.

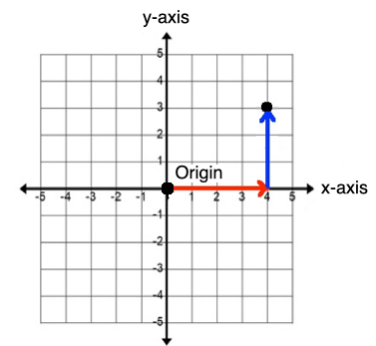
So far, we have been representing graphs of equations as a collection of points (x, y) in the Rectangular (Cartesian) Coordinate System. For example, in the picture below, we see the point (x, y) being (4, 3).

Now, we will study a second system called the Polar Coordinate System. The initial motivation for the introduction of the Polar Coordinate System was the study of circular and orbital motion. Polar coordinates are now used in navigation and for many phenomena in the physical world.

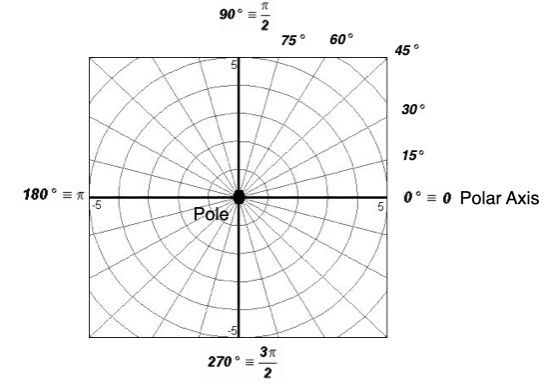
The Polar Coordinate System

Just like in the rectangular coordinate system we draw a horizontal and a vertical line that intersect at a right angle.The point where the lines intersect is no longer called the Origin, but the Pole.

Instead of rectangular gridlines, we now draw angles with their vertices at the Pole and their initial side at the polar axis. Their terminal sides are called r-axes. Equally spaced circles represent the "grid lines."

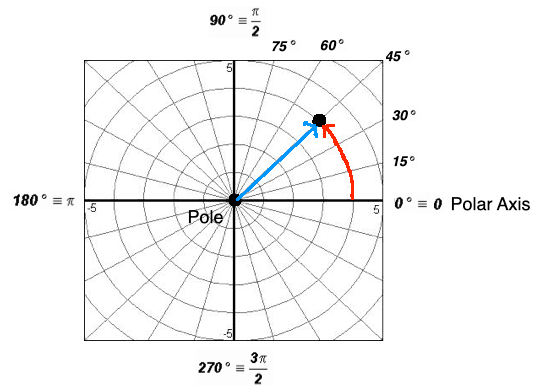
A point in the Polar Coordinate System is represented by the polar coordinates . The number r lies on an r-axis which is the terminal side of angle . For example, in the picture below, we see the point being (4, 45^o).

NOTES

1. The r-axis is positive along the terminal side of the angle and negative along the EXTENSION of the terminal side through the pole.

2. r and can be positive or negative.

3. can be expressed in radians or degrees.

Strategy for Graphing Points in the Polar Coordinate Systems - see #1 and 2 in the "Examples" document

• Starting at the polar axis, draw the angle to find its terminal side. This is the positive r-axis.
• Next, extend the terminal side of the angle through the pole. This is the negative r-axis.
• If r is positive, plot the point along the positive r-axis.
• If r is negative, plot the point along the negative r-axis.

In a Rectangular Coordinate System, there exists exactly one set of coordinates for each point. On the other hand, in a Polar Coordinate System, a point has infinitely many sets of coordinates.

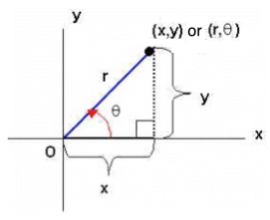
Formulas for Changing Rectangular Coordinates into Polar Coordinates and Vice Versa

It is often necessary to transform from rectangular to polar form or vice versa. The following relationships are useful in this regard.

NOTE: YOU MUST MEMORIZE THESE RELATIONSHIPS!

                   

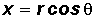
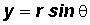
and the standard form of the equation of a circle with center at the origin:

They are derived from the following picture:

Strategy for Changing Polar Coordinates into Rectangular Coordinates - see #3 and 4 in the "Examples" document

• Sketch the point in the Polar Coordinate System to give you an idea of its location.
• Use the conversions and to find the rectangular coordinates.

Strategy for Changing Rectangular Coordinates into Polar Coordinates - see #5 through 8 in the "Examples" document

• Sketch the point (x, y) in the Rectangular Coordinate System to give you an idea of its location.
• Use the conversion to find the r-value. Depending on the instructions, use either the positive or negative r-value.
• Use the conversion to find the angle . Depending on the instructions and/or the location of the point, you may have to work with the Reference Angle to find the appropriate . Don't forget that Quadrantal Angles do not have Reference Angles!