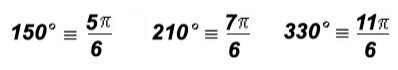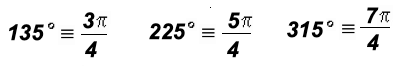INTRODUCTION TO ANGLES
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Define a ray and an angle.
2.   Memorize common angle names.
3.   Measure angles in degrees.
4.   Memorize types of angles in degrees and radians
      (zero-degree, right, straight, reflex, full).
5.   Measure angles in radians.
6.   Convert angles from degrees to radians and vice versa. There are three formulas that you must memorize!
7.   Know the difference between positive and negative angles.
8.   Define quadrantal angles in degrees and radians. Know their integer multiples.
9.   Define "special" angles and some of their integer multiples in degrees and radians.
10. Draw angles.
11. Find the location of angles in degrees and radians in the rectangular coordinate system.

Angles play a critical role in trigonometry. Therefore, we begin our study of trigonometry by looking at angles and methods for measuring them.

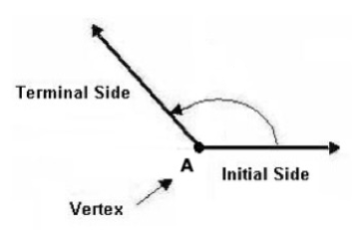
Definition of a Ray

A ray is a line that starts at one point and extends forever in one direction.

Definition of an Angle

An angle is determined by rotating a ray a specific distance about its starting point. The starting position of the ray is called the initial side of the angle. After the rotation we end up with another ray and it is called the terminal side of the angle. The point where the initial and the terminal side meet is called the vertex of the angle.

NOTE:  When drawing an angle, the rotation of the ray about its starting point is usually indicated with an arc in between the initial and terminal sides.

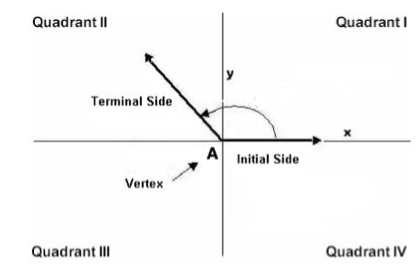
In trigonometry, we usually place an angle into a Rectangular Coordinate System with the initial side along the positive x-axis. We then say that the angle is in standard position.

Common Names of Angles

Often Greek letters are used to represent unknown angles. Most common are the following letters:

Theta:          Alpha:          Beta:          Gamma: 

Sometimes, angles are given the name of their vertex. In the picture above it would be angle A.

Angle Measure in Degrees

The measure of an angle is often called magnitude. In trigonometry, we measure angles in degrees or radians. We'll discuss degrees first. Later we will discuss radians.

We will know that angles are measured in degrees when there is little circle in the upper right-hand corner of a number.  For example, 45^o which is then pronounced 45 degrees. 

Degrees can further be divided into minutes ( ' ) and seconds ( " ). That is,

1^o = 60' (minutes) using the apostrophe on the computer keyboard

1' = 60" (seconds) using the quotation mark on the keyboard

Types of Angles

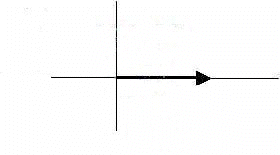
Zero-Degree Angle

An angle whose measure is 0^o is called a zero-degree angle.

NOTE:  The terminal side and the initial side are the same. There is no arc! 

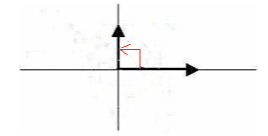
Right Angle

An angle whose measure is exactly 90^o is called a right angle.

Please note that a right angle is often indicated by drawing a square between the initial and the terminal side instead of an arc.

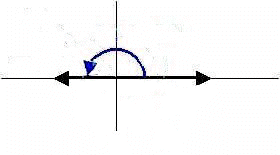
Straight Angle

An angle whose measure is exactly 180^o is called a straight angle.

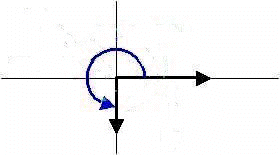
Reflex Angles

Angles whose measure is greater than 180^o but less than 360^o.

For example, 270^o.

 

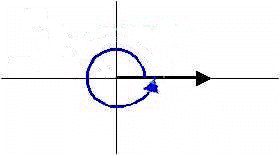
Full Angle

An angle whose measure is exactly 360^o.

NOTE:  The terminal side and the initial side are the same. Compare to a Zero-Degree angle. Unlike the angle, there is now an arrow indicating direction!

Acute Angles

Angles whose measure is greater than 0^o but less than 90^o.

Obtuse Angles

Angles whose measure is greater than 90^o but less than 180^o.

Angle Measure in Radians - see #1 through 6 in the "Examples" document

Unlike degrees, which use the "circle" symbol, radian measures use NO symbol. Later, in context, you will know when you are working with radians.

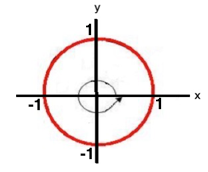
Radians are actually connected to the circumference (perimeter) of a unit circle which has a radius r of 1.

NOTE: We know from geometry that the circumference formula of a circle is . Given r = 1, the circumference of the unit circle is exactly .

Let's draw a unit circle into a rectangular coordinate system with center at the origin. Next, let's place an actue angle with measure a^o at its center as follows:

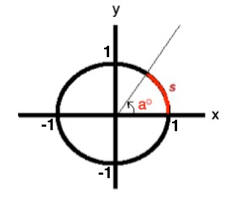
Note that the angle is opposite an arc s on the circle circumference. The length of arc s is considered the radian equivalent of a^o.

Now, let's draw another unit circle and place an angle with measure 360^o at its center as follows:

It should then be obvious that the size of the arc oppositve this angle is . This is considered the radian equivalent of the angle with measure . See picture below.

YOU MUST MEMORIZE THE FOLLOWING DEGREE-RADIAN CONVERSIONS:

1.

We use the "equivalent" symbol instead of the "equal" symbol because we are actually comparing "angles and lengths".

Please note, while 2 6.28, we usually DO NOT use the decimal equivalent.

2. Dividing the formula in #1 by 360, we get .

This formula is used to convert from degrees to radians. We usually do not convert to decimals, but leave the measure in terms of .

3. Solving the formula in #2 for 1 (radian), we get .

This formula is used to convet from radians to degrees.

Why use Radians?

As you move through more advanced topics in mathematics, physics, and engineering, you will discover that there are certain relationships that only work when radians are used.

Is Radian Measure always Expressed in terms of Pi?

In trigonometry, we like to work with radian measures containing a factor of such as . We call this an EXACT value.

However, be aware that in your studies you will also see radian measures expressed without a factor of . They would look just like regular numbers and can contain fractions, decimals, integers, etc.

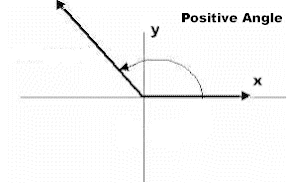
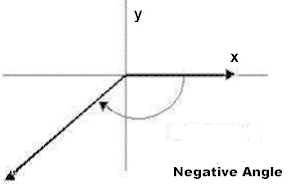
Positive and Negative Angles

In trigonometry, angles can have a positive or negative measure. Angles with positive measure are indicated by an arc drawn in counter-clockwise rotation. Please note the arrow at the end of the arc!

Angles with negative measure are indicated by an arc drawn in clockwise rotation. Please note the arrow at the end of the arc!

   

A word about negative angles ...

Please note that as a purely numerical statement is less than 10. However, in case of angles, the minus sign simply indicates orientation. Therefore, we may state that an angle measuring 10^o has a smaller magnitude than an angle measuring . 

Quadrantal Angles - see #7, 8, 14, and 15 in the "Examples" document

When the terminal side of angles lies along a coordinate axis, they are called Quadrantal Angles. They can be expressed in degrees and radians.

Most often used Quadrantal Angles:

0^o 0 (radians)                              

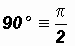
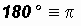
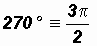
However, all angles that are integer multiples of are Quadrantal Angles.

YOU MUST MEMORIZE THESE QUADRANTAL ANGLES IN DEGREES AND RADIANS!

The following decimal approximations sometimes come in handy when using a calculator. By the way, always use the button on your calculator and never its decimal approximation 3.14!

                              

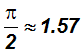
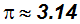
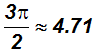
YOU MUST MEMORIZE THESE DECIMAL APPROXIMATIONS!

"Special" Angles - see #9 through 13, 16 and 17 in the "Examples" document

In trigonometry, three acute angles and their integer multiples show up over and over again. You will also find them in physics and engineering. They are often called "special" angles. They can be expressed in degrees and radians.

"Special" Angles:                    

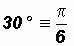
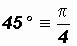
YOU MUST MEMORIZE THESE SPECIAL ANGLES IN DEGREES AND RADIANS!

Often used integer multiples of :

5(30^o) = 150^o and 7(30^o) = 210^o and 11(30^o) = 330^o

NOTE:

Often used integer multiples of :

3(45^o) = 135^o and 5(45^o) = 225^o and 7(45^o) = 315^o

NOTE:

Often used integer multiples of :

2(60^o) = 120^o and 4(60^o) = 240^o and 5(60^o) = 300^o

Please note that 120^o, 240^o, and 300^o are also integer multiples of 30^o. However, any time 60^o divides evenly into an angle measure, it is considered an integer multiple of 60^o.

NOTE:

YOU MUST MEMORIZE THESE INTEGER MULTIPLES OF SPECIAL ANGLES IN DEGREES AND RADIANS!

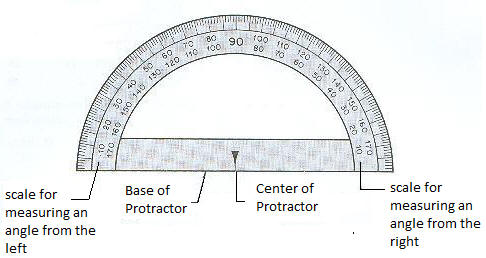
Drawing Angles - see #18 and 19 in the "Examples" document

We use a protractor to draw and measure angles up to 180^o.  Below is a picture of one type.  Note specifically the Base, the Center, and the Scale. When measuring angles, the Center is placed at the vertex of the angle with the Base along its initial side.

Note there are two scales, one for measuring acute angles and one for measuring obtuse angles.

If we wanted to draw an angle between 180^o and 360^o we would add an appropriate amount to the straight angle. For example, given 270^o we would add 90^o to 180^o.

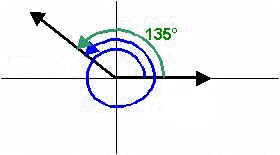
In trigonometry, we often deal with angles larger than 360^o. To graph such angles, we use circles to indicate the number of full angles found within these angles then ending with an arc for the remainder.

For example, we know that the angle 495^o is comprised of 360^o(1) + 135^o where 360^o(1) indicates one full angle.

We would graph 495^o as follows:

YOU MUST KNOW HOW TO GRAPH ANGLES IN DEGREES AND RADIANS!

The Location of Angles in the Rectangular Coordinate System - see #20 and 21 in the "Examples" document

The "location" of an angle is synonymous to the location of its terminal side.

• Angles with their terminal side in Quadrant I are called first-quadrant angles.
• Angles with their terminal side in Quadrant II are called second-quadrant angles.
• Angles with their terminal side in Quadrant III are called third-quadrant angles.
• Angles with their terminal side in Quadrant IV are called fourth-quadrant angles

YOU MUST BE ABLE TO FIND THE LOCATION OF THE TERMINAL SIDE OF ANGLES IN DEGREES AND RADIANS!