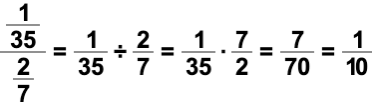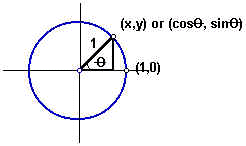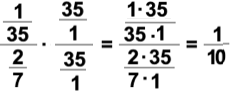SIMPLIFYING TRIGONOMETRIC EXPRESSIONS - PART 1
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
![]()
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Memorize fundamental trigonometric identities.
2. Simplify trigonometric expressions.
![]()
In trigonometry we are often asked to simplify trigonometric expressions. We do this primarily to make later work easier. For example, simplifying trigonometric expressions is often necessary when solving complex equations or when we "differentiate" and "integrate" in a calculus course.
One way to simplify trigonometric expressions is with the help of some "fundamental" trigonometric identities. We already discussed the importance of the Reciprocal and Quotient Identitites. But there are some others, particularly the Pythagorean Identities, which are also very important.
Fundamental Trigonometric Identities
Review - Reciprocal Identities
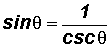
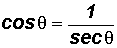
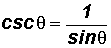
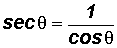
Review - Quotient Identities
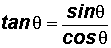
Pythagorean Identities
They are derived from the unit circle, which is a circle of radius 1.
Using the definitions of sine and cosine, we find that in the unit circle
and
.
The equation of the unit circle is
.
Then, we can rewrite the equation of the unit circle in trigonometric form as
where
and
.
This equation is usually rewritten in the following order with the sine ratio first:
In trigonometry, we usually write the exponent between the ratio and the angle, such as
.
YOU MUST MEMORIZE THE FOLLOWING SEVEN (7) PYTHAGOREAN IDENTITIES!
(1) The primary Pythagoran Identity is nothing but the equation of the unit circle in trigonometric form.
That is,
.
Please note that identities 2 through 7 below are derived from the primary Pythagorean Identity.
(2) If we subtract
from both sides of
, we get
(3) If we subtract
from both sides of
, we get
(4) If we divide every term of
by
, we get
(5) If we subtract 1 from both sides of
, we get
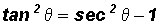
(6) If we divide every term of
by
, we get
(7) If we subtract 1 from both sides of
, we get
Simplifying Trigonometric Expressions - see #1 through 14 in the "Examples" document
We will now discuss the six most common methods used to simplify trigonometric expressions. Know them well! Note that sometimes you must use more than one method to most efficiently rewrite a trigonometric expression into its simplest form.
1. Use fundamental identities to rewrite trigonometric ratios and expressions.
2. Add or subtract trigonometric ratios. Know how to work with fractions!
3. Multiply trigonometric ratios and expressions.
4. Factor trigonometric expressions.
5. Separate fractions into two or more fractions.
6. Change complex fractions to simple fractions.
A fraction with fractions in the numerator, denominator, or in both is referred to as a complex fraction. We learned in arithmetic to always change complex fractions to simple fractions. We can do this in two different ways.
For illustration purposes, let's use the following complex fraction:
Method 1:
Simplify the complex fraction by multiplying it by a special form of the number 1.
In our case, the special form will be comprised of 35 as illustrated below.
Can you explain why we used 35 and not any other number?
Method 2:
Simplify the complex fraction by changing one of the fraction bars to the symbol
.
Then, we utilize the fact that dividing by a number is the same as multiplying by the reciprocal of the number.