INTRODUCTION TO CONIC SECTIONS - THE HYPERBOLA
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Change any hyperbola to standard form.
2.   Find the coordinates of the center, the foci, and the vertices.
3.   Find the length of the transverse and conjugate axes.

Let's continue our discussion of conic sections. In this lesson, we will discuss hyperbolas.

The Conic Section resulting in a Hyperbola - see #1 through 4 in the "Examples" document

The properties of hyperbolas can be used in radar and other detection systems. Another interesting application of conic sections involves the orbits of comets in our solar system. Of the 610 comets identified prior to 1970, 245 have elliptical orbits, 295 have parabolic orbits, and 70 have hyperbolic orbits. Comets with elliptical orbits, such as Halley's comet, are the only ones that remain in our solar system.

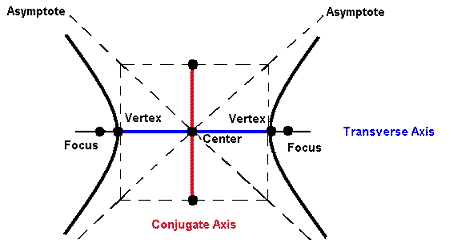
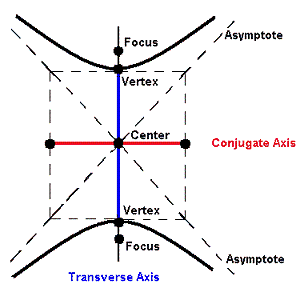
The definition of the hyperbola is based on two fixed points called the foci (singular: focus). Namely, for all points on the hyperbola, the absolute value of the difference of their distances from the two foci must be the same length.

The line through the foci intersects the hyperbola in two points called the vertices (singular: vertex). The line segment that joins the vertices is called the transverse axis which can be horizontal or vertical.

The two branches of the graph of a hyperbola approach a pair of intersecting straight lines called asymptotes. Both asymptotes pass through the midpoint of the transverse axis.

The center of the hyperbola is the midpoint of the transverse axis.

Often a rectangle is drawn through the vertices with corners at the asymptotes. The line segment perpendicular to the transverse axis intersecting it at its midpoint and with endpoints at the rectangle is called the conjugate axis.

Hyperbolas with a Horizontal Transverse Axis:

 

Standard Form of the equation is , where either a = b or a b.

You must know that this standard form with (x h)² being positive pertains to hyperbolas with a horizontal transverse axis.

You do not need to memorize the following information, however, you must know how to work with it when given.

Coordinates of the Center are (h, k).

Coordinates of the Foci are h + c, k) and (h c, k). The two foci each lie c units from the center, where .

Coordinates of the Vertices are (h + a, k) and (h a, k).

Note that a² is the denominator of the positive term which contains x !!!

Length of the Transverse Axis is 2a.

Note that a² is the denominator of the positive term which contains x !!!

Length of the Conjugate Axis is 2b.

Hyperbolas with a Vertical Transverse Axis:

 

Standard Form of the equation is , where either a = b or a b

You must know that this standard form with (y k)² being positive pertains to hyperbolas with a vertical transverse axis.

You do not need to memorize the following information, however, you must know how to work with it when given.

Coordinates of the Center are (h, k).

Coordinates of the Foci are (h, k + c) and (h, k c).The two foci each lie c units from the center, where .

Coordinates of the Vertices are (h, k + a) and (h, k a).

Note that a² is the denominator of the positive term which contains x !!!

Length of the Transverse Axis is 2a.

Note that a² is the denominator of the positive term which contains x !!!

Length of the Conjugate Axis is 2b.