SOLVING SIMPLE TRIGONOMETRIC EQUATIONS
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1.   Solve simple trigonometric equations on a restricted solution interval.
2.   Find ALL solutions of simple trigonometric equations.

In this lesson, we will learn how to solve simple trigonometric equations of the following forms:

asin(bx) = C

acos(bx) = C

atan(bx) = C 

Note that b = 1 and a and C are real numbers with a not equal to 0.

All trigonometric equations have infinitely many solutions! Often, the solutions are restricted to an interval in which case we may have zero to several solutions. Other times we are asked to find all solutions.

Solving Simple Trigonometric Equations on a Restricted Solution Interval - see #1, 2, 4 through 9 in the "Examples" document

Step 1:

Examine the solution interval and keep it in mind. If necessary, isolate the trigonometric ratio. "Isolate" means that the trigonometric ratio must be the only term on one side of the equal sign and its coefficient must be 1.

Step 2:

Use the Inverse Trigonometric Function concept to find a solution for the unknown angle. 

HINT:  If you are asked to find the EXACT radian solutions, it might be easier to convert to degrees!

Step 3:

If necessary, find the reference angle for the solution in Step 2. A reference angle will not exist if the solution in Step 2 is a quadrantal angle.

Step 4:

Find the solution(s) on the given solution interval.

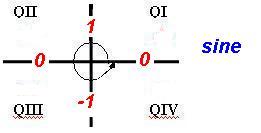
1. Examine the sign of the trigonometric ratio in Step 1. Is it positive or negative?

2a. If a reference angle exists in Step 3 and knowing the sign of the trigonometric ratio from Step 1, use this in conjuction with All Students Take Calculus to find the solution(s) on the given solution interval!

2b. If a reference angle does not exist in Step 3, we must know the values of the trigonometric ratios of quadrantal angles to find the solution(s) on the given solution interval.

          

 

Finding ALL Solutions of Simple Trigonometric Equations - see #3, 10 through 12 in the "Examples" document

Sometimes, we are not given a solution interval. Instead, we are asked to find ALL solutions. In that case, we do the following:

1. Find the solutions on the interval between 0 and or between 0^o and 360^o.
2. If the solutions in (1) are more than or 180^o apart, add 2k or 360^ok to each of these solutions, where k is any integer.
3. If the solutions in (1) are exactly or 180^o apart, add k or 180^ok to the smallest solution.