INTRODUCTION TO CONIC SECTIONS - THE ELLIPSE
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
![]()
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Change any ellipse to standard form.
2. Find the coordinates of the center, the foci, and the vertices.
3. Find the length of the major and the minor axes.
4. Distinguish between the conic section of a circle and an ellipse.
![]()
In this lesson, we will discuss the last two conic sections, namely the ellipse and the circle. Let's start with the ellipse.
The Conic Section resulting in an Ellipse - see #1 through 5 in the "Examples" document
Ellipses have many practical and aesthetic uses. For example, machine gears, supporting arches, and acoustical designs often involve elliptical shapes. The orbits of satellites and planets are also ellipses.
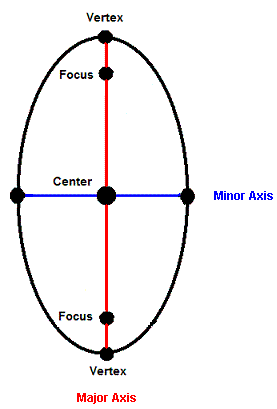
The definition of the ellipse is based on two fixed points called the foci (singular: focus). Namely, for all points on the ellipse, the sum of their distances from the two foci must be the same length.
The line through the foci intersects the ellipse in two points called the vertices (singular: vertex). The line segment that joins the vertices is called the major axis which can be horizontal or vertical. The line segment perpendicular to the major axis intersecting it at its midpoint and ending at the ellipse is called the minor axis. It can also be horizontal or vertical.
The center of the ellipse is the midpoint of the major axis.
Ellipses with a Horizontal Major Axis:
The Standard Form of the equation is
, where
.
You must know that this standard form with (x - h)2 having the greater denominator pertains to ellipses with a horizontal major axis.
You do not need to memorize the following information, however, you must know how to work with it when given.
Coordinates of the Center are (h, k).
Coordinates of the Foci are (h + c, k) and (h
c, k), where
.
Note that a2 is the larger denominator !!!
Coordinates of the Vertices are (h + a, k) and (h
a, k).
Note that a2 is the larger denominator !!!
Length of the Major Axis is 2a.
Note that a2 is the larger denominator !!!
Length of the Minor Axis is 2b.
Ellipses with a Vertical Major Axis:
The Standard Form of the equation is, where
.
You must know that this standard form with (y - k)2 having the greater denominator pertains to ellipses with a vertical major axis.
You do not need to memorize the following information, however, you must know how to work with it when given.
Coordinates of the Center are (h, k).
Coordinates of the Foci are (h, k + c) and (h, k
c), where
.
Note that a2 is the larger denominator !!!
Coordinates of the Vertices are (h, k + a) and (h, k
a).
Note that a2 is the larger denominator !!!
Length of the Major Axis is 2a.
Note that a2 is the larger denominator !!!
Length of the Minor Axis is 2b.
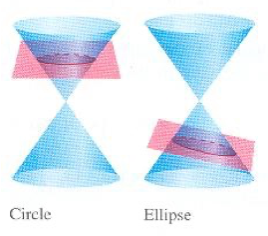
The Difference between the Conic Section of the Circle and the Ellipse
A plane parallel to the bottom of the stacked cones creates a circle. Whereas a slanted plane creates an ellipse.
The standard equation of the circle conic section is almost identical to the one for the ellipse conic section. The only difference is that the denominators a and b are identical. Unlike the ellpises where
.
Most of the time we express the standard form of a circle as we learned in algebra, namely (x
h)2 + (y
k)2 = r2 where (h,k) is the center and r is the radius.