POINT OF INTEREST 3
VALUES OF TRIGONOMETRIC RATIOS OF QUADRANTAL ANGLES
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to ingrid.stewart@csn.edu.

Let's derive the values of the sine,
cosine, and tangent ratios of the
angles with measures 0o, 90o, 180o, 270o, and 360o.
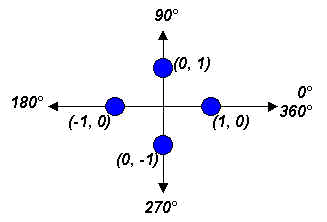
Let's place the point
(1, 0) on
the terminal side of the 0o and the 360o angle. On the terminal side of the 90o angle,we'll place the point
(0,
1). On the terminal side of the 180o angle
we'll place the point
( 1, 0), and on the terminal side of the 270o
1, 0), and on the terminal side of the 270o
angle we'll place the point
(0,
 1).
1).
We are using these points for
simplicity's sake! We could have used any other points lying on the
coordinate axes.
Now, we will use the definition of the trigonometric ratios in a novel way. That is, the x-coordinates of the points will be the "side adjacent", the y-coordinates of the points will be the "side opposite", and the "hypotenuse" will be the distance from the origin to each point. In our case, this distance is of length 1 to all points.
For example, using hyp = 1, we find
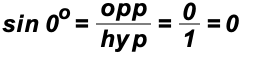 using point (1, 0)
using point (1, 0) 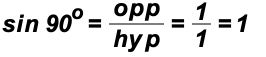 using point (0,
1)
using point (0,
1)
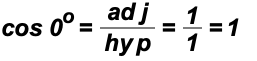 using point (1, 0)
using point (1, 0) 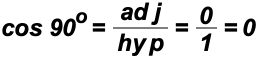 using point (0,
1)
using point (0,
1)
ETC.
YOU MUST MEMORIZE THE FOLLOWING VALUES!
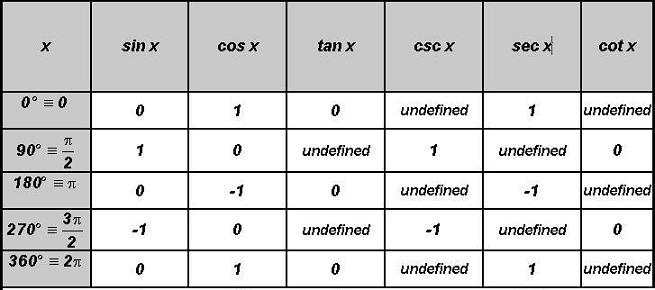
![]()
1, 0), and on the terminal side of the 270o

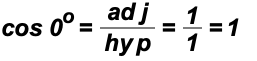 using point (1, 0)
using point (1, 0) 