POINT OF INTEREST 2
VALUES OF TRIGONOMETRIC RATIOS OF ANGLES OF ANY MAGNITUDE
Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Let's place a right triangle into the Rectangular Coordinate System so that the right angle lies opposite the origin.

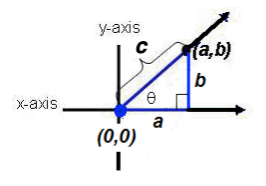
Observe that the length of leg a and the length of leg b produce the point (a, b) in the coordinate system and the hypotenuse c has length (Pythagorean Theorem).

For the subsequent discussion, we will use a 30-60-90 triangle. Specifically, we will draw right triangles containing a 30^o and 60^o angle into each quadrant of a coordinate system. We let the 60^o angle be next to the origin.

NOTE: We could have also used a 45-45-90 triangle.

Specific to our discussion, we will let the length of the side adjacent to angle 60^o equal x = 1 . From geometry we know that the hypotenuse of a 30-60-90 triangle is then of length 2x = 2(1) = 2, and the other leg is of length .

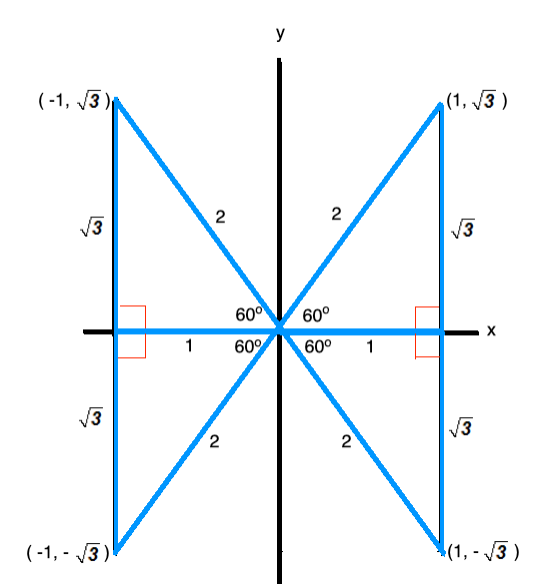
As we can see, these triangles produce the points , , , and .

Now, instead of using the sides of the triangles to define the values of the cosine, sine, and tangent ratios, we will use the four points stated above.

Their their x-coordinates will be equivalent to the sides adjacent, and their y-coordinates will be equivalent to the sides opposite the 60^o angle.

Angle 60^o

Its initial side is the positive x-axis, and we define its terminal side to be the line through the point in Quadrant I.

Using adj 1 and hyp 2, we find cos 60^o = .

Using opp and hyp 2, we find sin 60^o = .

Using opp and adj 1, we find tan 60^o = .

The secant, cosecant, and cotangent will all be positive.

Angle 120^o

Its initial side is the positive x-axis, and we define its terminal side to be the line through the point in Quadrant II.

Using adj 1 and hyp 2, we find cos 120^o = .

Using opp and hyp 2, we find sin 120^o = .

Using opp and adj 1, we find tan 120^o = .

The secant and cotangent will be negative and the cosecant will be positive.

Angle 240^o.

Its initial side is the positive x-axis, and we define its terminal side to be the line through the point in Quadrant III.

Using adj 1 and hyp 2, we find cos 240^o = .

Using opp and hyp 2, we find sin 240^o = .

Using opp and adj 1, we find tan 240^o = .

The secant and cosecant will be negative and the cotangent will be positive.

Angle 300^o.

Its initial side is the positive x-axis, and we define its terminal side to be the line through the point in Quadrant IV.

Using adj 1 and hyp 2, we find cos 300^o = .

Using opp and hyp 2, we find sin 300^o = .

Using opp and adj 1, we find tan 300^o = .

The cosecant and cotangent will be negative and the secant will be positive.

Do you notice in the above that some values are negative? As a matter of fact, we can actually establish the following pattern for any angle.

Do you further notice in the above that the multiples of angle 60^o produce values equal to the absolute value of the values in QI? This finding allows us to understand how some values of trigonometric ratios are connected.