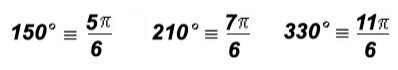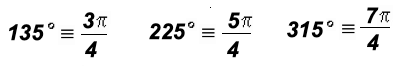Any Angles

TRIGONOMETRIC RATIOS OF ANGLES OF ANY MAGNITUDE - PART 2
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to ingrid.stewart@csn.edu.

Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!

1. Find reference angles in degrees and radians of given angles.
2. Find the exact values of trigonometric ratios of integer multiples of "special" angles without a calculator.

We are going to continue our discussion of trigonometric ratios of angles of any magnitude. Besides the quadrantal angles and their integer multiples, there is is one other set of angles that appear often in mathematics, physics, and engineering and those are the integer multiples of the "special" angles 30^o, 45^o, and 60^o.

It is common practice to teach trigonometry students how to find the EXACT values of the trigonometric ratios of integer multiples of special angles without using the calculator.

The following integer multiples occur frequently. You must memorize them. You must also memorize their radian equivalents.

Often used integer multiples of 30^o

5(30^o) = 150^o and 7(30^o) = 210^o and 11(30^o) = 330^o

NOTE:

Often used integer multiples of 45^o

3(45^o) = 135^o and 5(45^o) = 225^o and 7(45^o) = 315^o

NOTE:

Often used integer multiples of 60^o

2(60^o) = 120^o and 4(60^o) = 240^o and 5(60^o) = 300^o

Please note that 120^o, 240^o, and 300^o are also integer multiples of 30^o. However, any time 60^o divides evenly into an angle measure, it is considered an integer multiple of 60^o.

NOTE:

Reference Angles - see #1, 2, and 3 in the "Examples" document

Before we find the EXACT values of their trigonometric ratios without using the calculator, a discussion of reference angles is necessary.

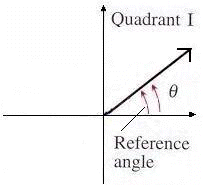
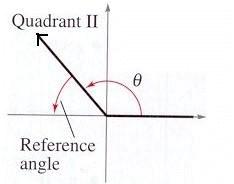
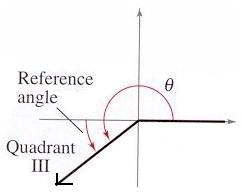
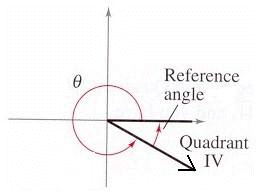
Reference angles are positive acute (less than 90^o) angles that lie between the terminal side of some angle and the horizontal axis in a coordinate system.

How to find a Reference Angle for some Angle :

Assume that is positive and between 0^oand 360^o (or 0 and ).

1. If is a first-quadrant angle, then the reference angle equals.

2. If is a second-quadrant angle, then the reference angle equals 180^o or .

3. If is a third-quadrant angle, then the reference angle equals 180^o or .

4. If is a fourth-quadrant angle, then the reference angle equals 360^o or .

Four Characteristics of Reference Angles:

The follwoing characteristics of reference angles will be stated without a formal proof. They should be evident from the discussion found under the link "Point of Interest 2" in the Learning Materials #4 in the MyOpenMath course.

1. The trigonometric ratio of an angle and that of its reference angle have the same ABSOLUTE value.

2. Negative angles have the same reference angles as their positive counterparts.

3. Coterminal angles have the same reference angle.

4. Quadrantal angles do not have reference angles.

Strategy for Finding EXACT Values of Trigonometric Ratios of Integer Multiples of Special Angles WITHOUT a Calculator - see #4 through 14 in the "Examples" document

Assume that angle is an integer multiple of a "special" angle.

Step 1:

Find the reference angle of the given angle . Might have to use one or more of the four characteristics of reference angles.

Step 2:

Find the value of the given trigonometric ratio of the reference angle from Step 1.

Step 3:

Find the value of the trigonometric ratio of the given angle with the help of the following:

the value found in Step 2

one or more of the four characteristics of reference angles

"All Students Take Calculus" on the given trigonometric ratio of angle

NOTE: Some students who have had trigonometry in the past might have memorized the following unit circle.

It is NOT a good idea to memorize the coordinates of the points in the picture above! Using Reference Angles is necessary for later concepts as well and anyone who refuses to learn it now will be in trouble later on! So please, do not use your unit circle coordinates.