TRIGONOMETRIC RATIOS OF ANGLES OF ANY MAGNITUDE - PART 1
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to
ingrid.stewart@csn.edu.
Learning Objectives - This is what you must know after studying the lecture and doing the practice problems!
1. Find coterminal angles in degrees and radians of given angles and vice versa.
2. Memorize when trigonometric ratios have positive and negative values.
3. Memorize the values of trigonometric ratios of quadrantal angles.
4. Find the exact values of trigonometric ratios of integer multiples of quadrantal angles without a calculator.
In the previous lecture, we limited our discussion to values of trigonometric ratios of acute positive angles. In this lesson, we will begin a discussion of trigonometric ratios of angles of any magnitude, positive and negative. However, we before we do so we must introduce the concept of coterminal angles.
Coterminal Angles - see #1 through 5 in the "Examples" document
Angles with the same initial and terminal side are called coterminal angles. For example, the angles with measure of 0o
0 and
are coterminal.
and
We find the coterminal angles of an angle
by adding to it integer multiples of 360o or
depending on the angle measure. We usually express angles coterminal to angle
NOTE: The letter k is often used to indicate the integer, however, other letters can be used as well.
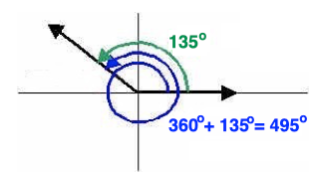
Please examine the picture below! We can see that 360o added to 135o results in an angle that has the same initial and terminal side, namely 495o. We can say that 495o is coterminal with 135o.
YOU MUST MEMORIZE HOW TO FIND COTERMINAL ANGLES OF GIVEN ANGLES AND VICE VERSA!
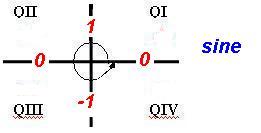
Positive and Negative Values of Trigonometric Ratios - see #6 and 7 in the "Examples" document
Using the calculator, we quickly notice that the values of trigonometric ratios can be positive or negative when the magnitude of an angle is larger than 90o. For example, sin 200o is approximately equal to
0.342 while sin (
So when are trigonometric ratios positive and when are they negative?
There is actually a pattern! It is summarized in the table below and it was developed in the documents found under the link "Point of Interest 2" in the Learning Materials #4 in the MyOpenMath course.
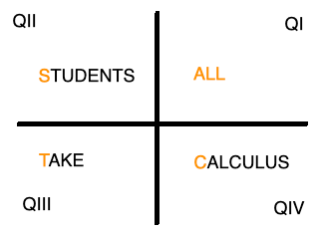
The pattern above must be memorized! Following is a handy memorization aid we call "All Students Take Calculus". It lets us know in which quadrant the value of the trigonometric ratio of an angle is positive.
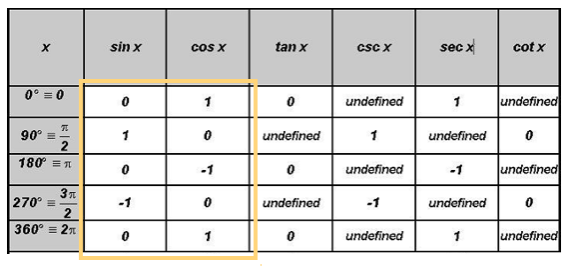
Values of Trigonometric Ratios of Quadrantal Angles
We already mentioned the quadrantal angles 0o, 90o, 180o, 270o, and 360o and we were told that they are often used in trigonometry, physics, and engineering.
Of course, we can find the values of trigonometric ratios of quadrantal angles with a calculator. However, they appear often in mathematics, physics, and engineering, therefore, it is common practice to require trigonometry students to memorize them.
In the table below find the values of the trigonometric ratios of the quadrantal angles. If you are interested where these values come from, please read the documents found under the link "Point of Interest 3" in the Learning Materials #4 in the MyOpenMath course.
YOU MUST MEMORIZE THE VALUES OF ALL TRIGONOMETRIC RATIOS GIVEN THE FOLLOWING ANGLES!
Memorization Hint: Only memorize the values for sine and cosine. Please note the special pattern of 0's, and 1's. Use the Reciprocal and Quotient Identities to find the values for the remaining trigonometric ratios.
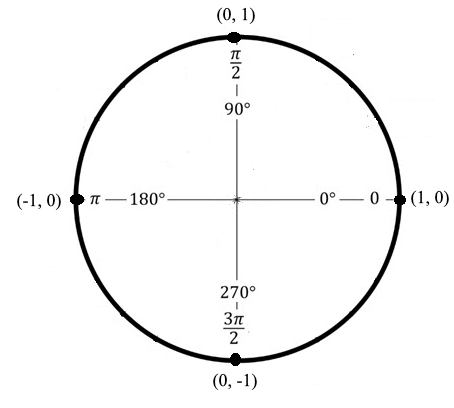
Some students who have had trigonometry in the past might have memorized the values in the table above using the unit circle.
The x-coordinates of the points on the circle above are the values of cosine of quadrantal angles and the y-coordinates are the values of sine. The values of the tangent can be calculated using the Quotient Identity.
Some Calculator "Odditites" - see #8, 9, and 10 in the "Examples" document
In the table above, some of the values of trigonometric ratios of quadrantal angles are undefined. When we evaluate these ratios with a calculator, most will tell us "domain error." Some calculators show the infinity symbol
.
The biggest issue arises when we want to evaluate the cotangent of some quadrantal angles. When we use the Reciprocal Identity most calculator will incorrectly state "domain error" even though the value of the cotangent is actually 0. Therefore, it is best to use the Quotient Identity when evaluating the cotangent with the calculator!
Strategy for Finding EXACT Values of Trigonometric Ratios of Integer Multiples of Quadrantal Angles WITHOUT a Calculator - see #11 through 14 in the "Examples" document
Of course, we can find these values with a calculator. However, they appear often in mathematics, physics, and engineering, therefore, it is common practice to require trigonometry students to find them without a calculator..
Assume that angle
has a magnitude of 90ok
180o
Step 1:
Find the angle
coterminal with angle
.
Step 2:
Use the fact that the values of trigonometric ratios of coterminal angles are identical.
Reminder:
