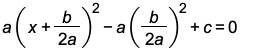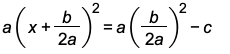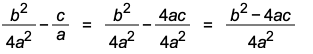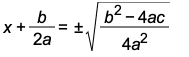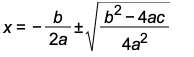POINT OF INTEREST

Copyright by Ingrid Stewart, Ph.D.  Please Send Questions and Comments to ingrid.stewart@csn.edu.

Create the Quadratic Formula .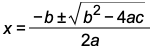

Let's solve the General Form of the quadratic equation for x.

This is done using the Square Root Property, but first we will have to change the General Form to the form .

Step 1:

Factor a out of the General Form as follows:

Step 2:

Use the Perfect Squares formula (A + B)(A + B) = A² + 2AB + B² and create a perfect square inside the parentheses.

In our case, A = x. We must change the middle term to 2(x)(?), namely to . This makes the last term B equal to .

To create a perfect square, we must add B², namely . But because of the a outside the brackets, we must actually add .  

To preserve the value of we must then subtract again as follows:

We get .

Step 3:

We will now factor the perfect squares expression in the brackets to get the following 

Please note that is a constant term (no x's).

Step 4:

Now let's use the Square Root Property to solve the equation in Step 3 for x.

We will move the constant term to the right side of the equal sign as follows:

Next, we will divide both sides by a as follows:

which can be simplified to .

We will continue to simplify the fraction on the right of the equal sign. Study it carefully! All we did was fraction operations!

Then we can write .

Finally, we are ready to apply the Square Root Property to get

Now we will isolate the x as follows:

Finally, we will do some major "clean-up" to arrive at the Quadratic Formula. Study the square root and fraction manipulations carefully!

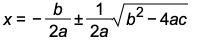
and we end up with the Quadratic Formula .