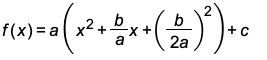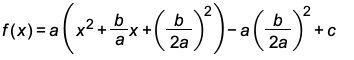POINT OF INTEREST
Copyright by Ingrid Stewart, Ph.D. Please Send Questions and Comments to ingrid.stewart@csn.edu.
![]()
Given the Standard Form ![]() of the quadratic function, the coordinates of the vertex point (h, k).
of the quadratic function, the coordinates of the vertex point (h, k).
Given the General Form ![]() of the quadratic equation, the vertex point is
of the quadratic equation, the vertex point is 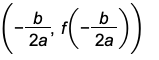 .
.
![]()
Proof that ![]() .
.
Let's change the general form of the quadratic function to standard form using the Completing the Square Method.
First, we will factor a out of the general form as follows:
Now we are ready to complete the square.
Please note that we added
to complete the square INSIDE the brackets.
But because of the a outside the brackets, we actually added
.
Therefore, to preserve equality, we must then subtract
OUTSIDE the brackets.
Finally, we factor the expression in the brackets to get the standard form of the quadratic function.
That is,
.
Since the standard form is usually written with a minus sign inside the parentheses, we will change the plus sign to
as follows:
, where
and
.