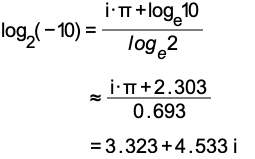What is the value of log_b0?

As we know, a logarithm can only be defined if the base b is greater than 0.

For a moment, let's assume that a logarithm argument equals 0, and let's log_b0 be equal to some number n, that is, log_b0 = n.

In its exponential form this would be 0 = bⁿ.

You are challenged to find a base b and an exponent n for which this is true!!! What about if n euqals 0? But any number b raised to a 0 power has a value of 1. What about if n is a negative number? But any number b raised to a negative number is a fraction.

You will find that there is no such power n that would make an exponential expression be equal to 0 given a base b greater than 0.

Therefore, log_b0 is not defined.

What is the value of log_b(a)?

Logarithms of negative numbers are not defined in the real numbers. If you are expected to find the logarithm of a negative number, an answer of "undefined" is sufficient in most cases.

However, it is possible to evaluate a logarithm of negative numbers. The answer will be a complex number, a number of the form a + bi, where i is the imaginary number equal to .

For a moment, let's assume that the logarithm argument is a negative number, say a, and let's log_b(a) be equal to some number n, that is, log_b(a) = n. We will further assume that base b is not equal to the number e.

Now let's use the Change-of-Base Property to change log_b(a) to base e.

Note that log_e (a) is the the same thing as log_e (1 a). We can now use the Product Rule of logarithms to write the numerator as follows:

log_e (a) = log_e (1 a)

                = log_e (1) + log_e a

and

Now the only problem is figuring out what log_e (1) is equal to. It might look like an impossible thing to evaluate at first, but there is a pretty famous equation known as Euler's Identity that can help us.

Euler's Identity states:

This result comes from Calculus and is a power series expansions of sine and cosine. We won't explain that too in-depth, but if you are interested, there is a nice page here which explains a bit more.

For now, let us simply take the natural logarithm of both sides of Euler's Identity:

Using th basic logarithm property log_bb^x = x, we find

So now that we know what log_e (1) is equal to, we can substitute it back into the equation

That is,

Now we have a formula for finding logarithms of negative numbers.

For example, if we were asked to find log₂(10) and round the answer to three decimal places, we would get